Question

The masses of the blocks A,B, and C shown in the fig. (a) are $4kg$, $2kg$, and $2kg$, respectively. Block A moves with an acceleration of $2.5m{s^{ - 2}}$.
1. Block C is removed from its position and placed on block A, shown in fig(b). What is the acceleration of block C?
2. The positions of the block A and B are subsequently interchanged. Find the new acceleration of C. The coefficient of friction is the same for all the contact surfaces.

Answer 1

To solve the question, free body diagrams of each block are to be drawn in both cases. The net forces are equated in x-direction and y-direction to find the acceleration of the block C. The first step is to calculate the coefficient of friction.

Complete step by step solution:
It is given in the question that-
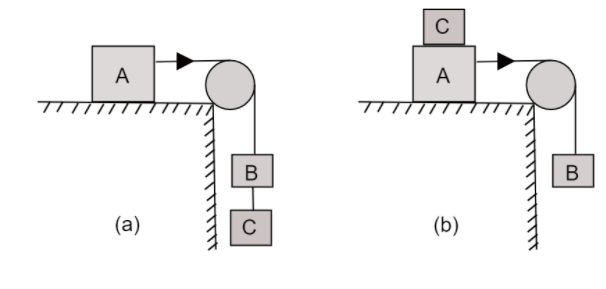
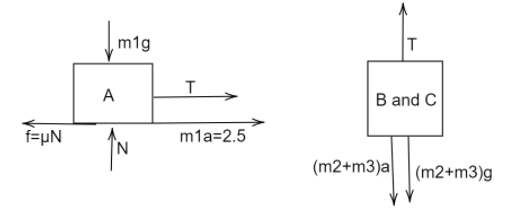
Acceleration of the block A is $2.5m/{s^2}$, if the pulley is assumed to be frictionless then B and C also accelerate with the same rate, because they are connected by the same string.
On drawing the Free body diagrams of A and B-C

We have,
Force of friction $f = \mu N$
The normal force exerted by the surface on block A$= N$
$N = {m_1}g = 4g$
Tension in the string $= T$
The value of g is taken $10m/{s^2}$for all calculations.
Mass of block A ${m_1} = 4kg$
Masses of block B and C added, as they are considered to be a system of mass, ${m_2} + {m_3} = 2 + 2 = 4kg$
Acceleration of the blocks a, it is $2.5m/{s^2}$.
Equating for block A-
In the vertical direction,
${m_1}g = N=4g$
In horizontal direction-
$T = \mu N - {m_1}a$
$T = 4\mu g - 4 \times 2.5$ …..…(1)
For block B and C,
In vertical direction,
$T = ({m_2} + {m_3})(g + a)$
$T = 4(g + a)$
$T = 4g + (2.5 \times 4)$ ……..…(2)
Equating equations (1) and (2),
$T = 4g + 10 = 4g\mu - 10$
$4g(1 - \mu ) = 20$
$\mu = 0.5$
Using this value of $\mu$, in case(a),
The Free body diagram is-

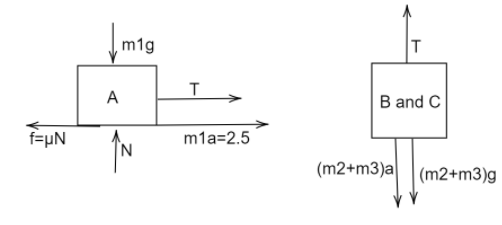
When the body C is placed on A, there is a friction force between the two bodies that act on C and A due to inertia of the block C, but it is small and cancels out when block A and C are assumed to be moving together with an acceleration downwards (+).
For the system A and C,
In horizontal direction,
$\mu N = ({m_1} + {m_3})a + T$
In vertical direction,
$N = ({m_1} + {m_3})g$
$N = 6g = 60$
$\mu N = 30$
$T - 30 = 6a$ ………(1)
For the block B,
In vertical direction,
${m_2}g - T = {m_2}a$
$20 - T = 2a$ ………..…(2)
Equating the above equations,
$20 - 2a = 6a + 30$
$6a + 2a = 8a = - 10$
$a = - 0.8$
The value of a is negative, this means the direction of assumed acceleration was not correct this implies that no acceleration takes place in the first case. Because the acceleration in the opposite direction is not possible. So, $a=0$.

(b) When A and B are interchanged, the Free body diagram becomes-

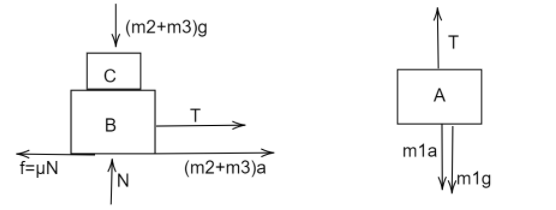
The blocks B and C are assumed to move together, with an acceleration a, then block A moves with the same acceleration, downwards(+).
For the system C and B,
In vertical direction,
$({m_2} + {m_3})g = N$
In horizontal direction,
$T - \mu N = (m2 + m3)a$
$\mu N = 4\mu g = 4 \times 0.5 \times 10 = 20$
$T - 20 = 4a$ …….…(1)
For the block A,
In vertical direction,
${m_1}g - T = {m_1}a$
$40 - T = 4a$ ……….…(2)
On solving both the equations,
$T = 40 - 4a = 4a + 20$
$8a = 20$
$a = 2.5m/{s^2}$
Checking for slip on the block C- There is a pseudo force between the blocks B and C, which arises due to the acceleration of blocks, if this is more than the minimum value of kinetic friction the block C will slip in the right direction.
Therefore, Pseudo force $F' = {m_3}a = 2 \times 2.5 = 5$
The maximum value of static friction $f' = \mu N = \mu {m_3}g = 0.5 \times 2 \times 10 = 10$
$F' < f'$ thus the block will not slip.
All units of force are in Newton.

Note: The pseudo force arises only in a non-inertial frame of reference, in the given question, part (b) the block B is accelerating, and the block C lies on top of it. Which means the block C is in a non-inertial frame of reference.