Question

The mass of the bob of a simple pendulum of length L is m. If the bob is left from its horizontal position then the speed of the bob and the tension in the thread in the lowest position of the bob will be respectively.

& \text{A}\text{. }\sqrt{2gL}\text{ and }3mg \\\ & \text{B}\text{. }3mg\text{ and }\sqrt{2gL} \\\ & \text{C}\text{. }2mg\text{ and }\sqrt{2gL} \\\ & \text{D}\text{. }2gL\text{ and }3mg \\\ \end{aligned}$$

Answer 1

We can redraw the given diagram and name the horizontal and the lowest position. While going from its initial position to the lowest position some work is done and from work energy theorem we can find the speed of the bob. As the bob has a circular motion there will be centripetal force and hence by balancing the force we can find the tension in the thread.

Formula used: $W=\Delta K.E.$
${{F}_{c}}=\dfrac{m{{v}^{2}}}{r}$

Complete step by step answer:
We can name the horizontal position as A and the lowest position B and show the forces which will be acting on the bob at its lowest position and redraw the given diagram.

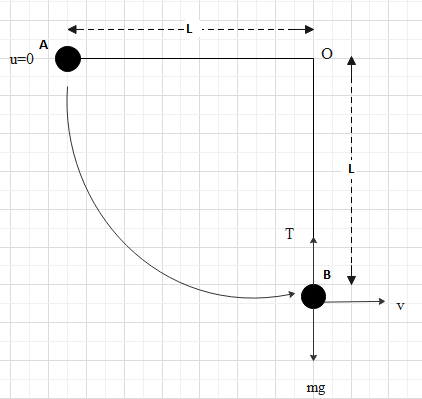
Now, at position A from where the bob is released the initial velocity will be zero, say $u=0$and when it reaches at B the velocity will change, say v. Some work will be done by the bob while going from A to B, from the work energy theorem
$W=\Delta K.E.$
Where work done is given by change in kinetic energy of the bob. We can write the above theorem as
$W=\dfrac{1}{2}m{{v}^{2}}-\dfrac{1}{2}m{{u}^{2}}$
As initially the velocity was zero and $u=0$, which implies
$W=\dfrac{1}{2}m{{v}^{2}}$
Now the work done can be given as the energy stored in the bob in the form of potential energy.
$mgL=\dfrac{1}{2}m{{v}^{2}}$
Where m is the mass of the bob, g is acceleration due to gravity, v is the velocity of bob at position B and L is the length of the thread from which bob is attached. As we have to find the speed of bob, we can rewrite the above equation in form of v

& {{v}^{2}}=\dfrac{2mgL}{m} \\\ & {{v}^{2}}=2gL \\\ & v=\sqrt{2gL} \\\ \end{aligned}$$ Hence the speed of the bob when released from position A is $$\sqrt{2gL}$$ Now let us consider the forces acting on the bob at position B, the upward tension T in the thread and downward gravitational pull mg and there will be centripetal force due to its circular motion, by balancing the forces we can write. $$\dfrac{m{{v}^{2}}}{L}=T-mg$$ Where $$\dfrac{m{{v}^{2}}}{L}$$ is the centripetal force. We can rewrite the equation in terms of T, $$T=\dfrac{m{{v}^{2}}}{L}+mg$$ Substituting value of v we deduced above, the equation becomes $$\begin{aligned} & T=\dfrac{m(2gL)}{L}+mg \\\ & T=2mg+mg \\\ & T=3mg \\\ \end{aligned}$$ Hence tension in the thread is 3mg. **So, the correct answer is “Option A”.** **Note:** Here we have calculated the work done by the simple pendulum from position A to B and not for one complete oscillation. Work done for one complete oscillation will be zero. As work done is given as force multiplied by displacement and for one complete oscillation displacement is zero and hence work done for one complete oscillation will be zero.