Question

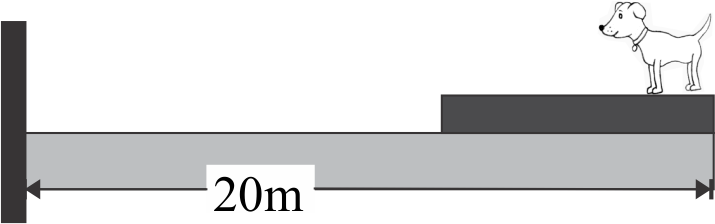
The mass of the boat is $40kg$ and friction between the boat and water surface is negligible. If the mass of a dog standing on a flat $10m$ long boat is $10kg$ such that it is $20m$ from the shore and walks $8m$ towards the shore on the boat and then stops. Then find the distance of the dog from the shore.

Answer 1

Centre of mass of the system will remain stationery. Find the initial distance of center of mass of the boat from the shore. The boat has to move away from the shore when the dog moves towards the shore.

Complete step by step solution:
Assume the dog and boat as a system.
Center of mass will be at rest initially. The center of mass of the system will remain stationery as no external force is applied on the system.
Let the distance of the center of mass of the boat from the shore initially be $x$ meter. So, -
$\Rightarrow {x_{1.cm}} = \dfrac{{40 \times x + 10 \times 20}}{{40 + 10}}m \cdots \left( 1 \right)$
where, ${x_{1.cm}}$ is the distance of the center of mass of the system from the shore.
As given in the question, that the dog moves towards the shore. The boat has to move away from the shore as the center of mass of the system will be at rest. Then, let the distance moved be denoted by $x'$
$\Rightarrow {x_{2.cm}} = \dfrac{{40\left( {x + x'} \right) + 10\left( {20 - 8 + x'} \right)}}{{40 + 10}} \cdots \left( 2 \right)$
Now, according to the question, we know that, -
${x_{1.cm}} = {x_{2.cm}} \cdots \left( 3 \right)$
Using equation (1) and (2), we get in the equation (3), we get –
$\Rightarrow \dfrac{{40x + 200}}{{50}} = \dfrac{{40\left( {x + x'} \right) + 10\left( {12 + x'} \right)}}{{40 + 10}} \\\ \Rightarrow \dfrac{{40x + 200}}{{50}} = \dfrac{{40x + 40x' + 120 + 10x'}}{{50}} \\\$
Cancelling 50 on denominator from the both sides and solving, we get –
$\Rightarrow 40x + 200 = 40x + 40x' + 120 + 10x' \\\ \Rightarrow 50x' = 80 \\\ \Rightarrow x' = 1.6m \\\$
Hence, the distance of the dog from the shore is
$\Rightarrow 20 - 8 + 1.6 \\\ \Rightarrow 13.6m \\\$
Note: Center of mass is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point where force may be applied to cause linear acceleration without an angular acceleration.