Question

The mass of a simple pendulum bob is 100gm.The length of the pendulum is 1m. The bob is drawn aside from the equilibrium position so that the string makes an angle of $60{}^\circ$ with the vertical and let go. The kinetic energy of the bob while crossing its equilibrium position will be:
(A)1J
(B)0.49J
(C)0.94J
(D)1.2J

Answer 1

The pendulum moves under the influence of restoring force. The tension in the string is always directed towards the centre. We can exploit the law of conservation of energy here to arrive at our solution.

Complete step by step answer:
The situation can be described in the free body diagram below;

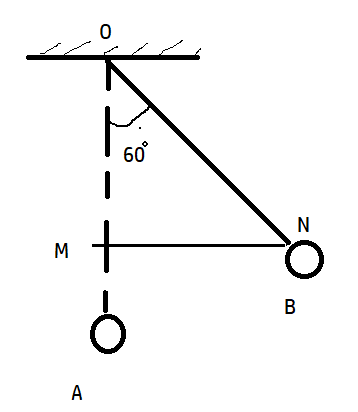
A is the equilibrium position of the pendulum and currently, it is held at B making an angle of $60{}^\circ$with the vertical.
m=100g
m=0.1Kg
Length of the pendulum, l=1m
When the bob is released from point B, because of restoring force it has the tendency to move towards the equilibrium position. We can use trigonometry to find out the length OM

& \cos 60{}^\circ =\dfrac{OM}{ON} \\\ & 0.5=\dfrac{OM}{1} \\\ & OM=0.5m \\\ \end{aligned}$$ Now potential energy at point B is given by, $$\begin{aligned} & {{U}_{B}}=mg{{l}_{1}} \\\ & =mg \\\ \end{aligned}$$ Now potential energy at point A is given by, $$\begin{aligned} & {{U}_{A}}=mg{{l}_{2}} \\\ & =0.5mg \\\ \end{aligned}$$ Change in energy, $$\begin{aligned} & \Delta U={{U}_{B}}-{{U}_{A}} \\\ & =mg-0.5mg \\\ & =0.5mg \\\ \end{aligned}$$ This energy is converted into kinetic energy $$\begin{aligned} & \Rightarrow \dfrac{m{{v}^{2}}}{2}=0.5mg \\\ & =0.5\times 0.1\times 9.8 \\\ & =0.49J \\\ \end{aligned}$$ Hence the kinetic energy of the bob at equilibrium position is 0.49J. So, the correct option is (C) **Note:** While substituting the values we have to be careful that all the units are in SI. Also, there is no external force present here, so there is no loss of energy. If some external force would have been present we would then have to consider the energy loss against that force.