Question

The marks obtained by 100 students of a class in an examination are given below.

Marks	$0 - 5$	$5 - 10$	$10 - 15$	$15 - 20$	$20 - 25$	$25 - 30$	$30 - 35$	$35 - 40$	$40 - 45$	$45 - 50$
No. of Students	$2$	$5$	$6$	$8$	$10$	$25$	$20$	$18$	$4$	$2$

Draw a less than type Cumulative Frequency Curve (Ogive). Hence Find the Median.

Answer 1

In this question we will convert the frequency table to a cumulative frequency table and plot the graph and then draw its ogive, and hence find the median.

Complete step-by-step solution:
To draw an ogive we require the cumulative frequencies of the values
The distribution table can be written as:

Marks	No. of Students
$0 - 5$	$2$
$5 - 10$	$5$
$10 - 15$	$6$
$15 - 20$	$8$
$20 - 25$	$10$
$25 - 30$	$25$
$30 - 35$	$20$
$35 - 40$	$18$
$40 - 45$	$4$
$45 - 50$	$2$

Now to find the Cumulative frequencies in a less than type cumulative frequency we add all the preceding terms to the current term, Therefore the cumulative frequency table could be written as:

Marks	No. of Students	Cumulative Frequency
$0 - 5$	$2$	$2$
$5 - 10$	$5$	$2 + 5$
$10 - 15$	$6$	$2 + 5 + 6$
$15 - 20$	$8$	$2 + 5 + 6 + 8$
$20 - 25$	$10$	$2 + 5 + 6 + 8 + 10$
$25 - 30$	$25$	$2 + 5 + 6 + 8 + 10 + 25$
$30 - 35$	$20$	$2 + 5 + 6 + 8 + 10 + 25 + 20$
$35 - 40$	$18$	$2 + 5 + 6 + 8 + 10 + 25 + 20 + 18$
$40 - 45$	$4$	$2 + 5 + 6 + 8 + 10 + 25 + 20 + 18 + 4$
$45 - 50$	$2$	$2 + 5 + 6 + 8 + 10 + 25 + 20 + 18 + 4 + 2$

Upon simplifying the above table, we get:

Marks	No. of Students	Cumulative Frequency
$0 - 5$	$2$	$2$
$5 - 10$	$5$	$7$
$10 - 15$	$6$	$13$
$15 - 20$	$8$	$21$
$20 - 25$	$10$	$31$
$25 - 30$	$25$	$56$
$30 - 35$	$20$	$76$
$35 - 40$	$18$	$94$
$40 - 45$	$4$	$98$
$45 - 50$	$2$	$100$

Now, we have to plot the graph with taking the upper limit of Marks on X-axis and the respective cumulative frequency on the Y-axis to get the less than ogive.
The points to be plotted to make a less than ogive are on the graph are: $(5,2),(10,7),(15,13),(20,21),(25,31),(30,56),(35,76),(40,94),(45,98),(50,100)$

The Curve in the above graph is the Cumulative Frequency Curve i.e. The ogive.
Now to find the median:
Let $N$ be the total number of students whose data is given.
Also $N$ will be the cumulative frequency of the last interval.
We find the ${\left[ {\dfrac{N}{2}} \right]^{th}}$ item (student) and mark it on the y-axis.
In this case the ${\left[ {\dfrac{N}{2}} \right]^{th}}$ item (student) is ${(100/2)^{th}}$ = ${50^{th}}$ student.
We draw a perpendicular from $50$ to the right to cut the Ogive curve.
From where the Ogive curve is cut, draw a perpendicular on the x-axis. The point at which it touches the x-axis will be the median value of the series as shown in the graph:

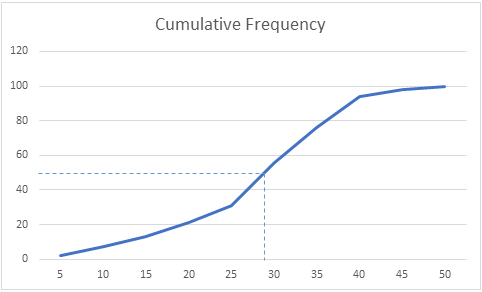
$\therefore$ From the above Graph we can see that the median is $29$
Hence we get the required answer.

Note: The cumulative frequency should always be plotted on the Y-axis to get a correct ogive.
There also exists a more than ogive, in this type of ogive while making the cumulative frequency table, all the succeeding terms in the distribution should be added to a term in the table.