Question

The magnitude of the induced electric field inside the solenoid, at a distance $r < R$ from its long central axis is:

A. $\dfrac{{3{\mu _0}n{I_{\max }}\omega }}{2}r\,\sin \omega t$
B. $\dfrac{{{\mu _0}n{I_{\max }}\omega }}{2}r\,\cos \omega t$
C. ${\mu _0}n{I_{\max }}\omega r\,\sin \omega t$
D. $\dfrac{{{\mu _0}n{I_{\max }}\omega }}{2}r\,\sin \omega t$

Answer 1

A cylindrical coil of many tightly wound turns of insulated wire with a general diameter of the coil smaller than its length is called a solenoid. Each turn in a solenoid is regarded as a circular loop. Here, we will use the formula of faraday’s law to calculate the electric field.

Complete step by step answer:
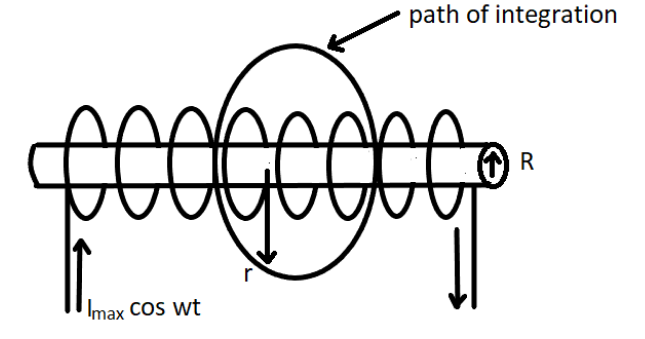
Consider a very long solenoid having $n$ turns per unit length of the solenoid. Let the current $I$ be flowing through the solenoid.

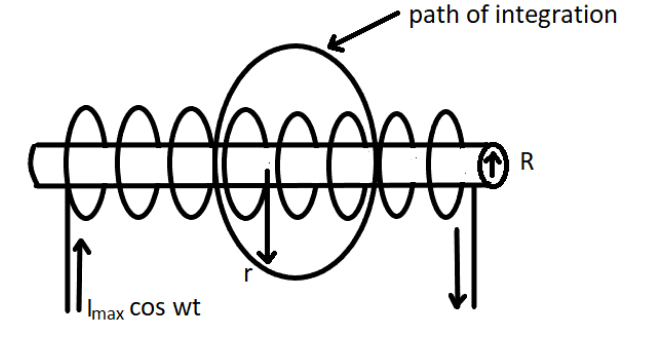
The figure above shows the magnetic field inside the solenoid is almost uniform, strong, and directed along the axis of the solenoid. Now, if the solenoid has $n$ turns than the magnetic field inside the solenoid is given by
$B = {\mu _0}nI$

Now, according to faraday’s law, the induced EMF in the solenoid is given by
$\oint {\vec E.d\vec l = \dfrac{{ - d{\phi _m}}}{{dt}}}$
Taking magnitude on both sides, we get
$\left| {\oint {\vec E.d\vec l} } \right| = \left| {\dfrac{{d{\phi _m}}}{{dt}}} \right|$

Now, flux inside the solenoid of the radius $r$ is given by
$\phi = \int {B.ds}$
Putting the value of $B$ we get
$\phi = \int {{\mu _0}nI.ds}$
$\Rightarrow \,\phi = \,{\mu _0}nI\int {ds}$
$\Rightarrow \,\phi = {\mu _0}nI(\pi {r^2})$

Now, putting this value of flux in the above equation, we get
$\left| {\oint {\vec E.d\vec l} } \right| = \left| {\dfrac{{d({\mu _0}nI\pi {r^2})}}{{dt}}} \right|$
$\Rightarrow \,\vec E\oint {d\vec l\, = \left| {{\mu _0}n\pi {r^2}\dfrac{{dI}}{{dt}}} \right|}$
$\Rightarrow \vec E(2\pi r) = \left| {{\mu _0}n{r^2}\dfrac{{d\left( {{I_{\max }}\cos \omega t} \right)}}{{dt}}} \right|$
$\Rightarrow \vec E(2\pi r) = \left| {{\mu _0}n{r^2}{I_{\max }}\omega \,\sin \omega t} \right|$
$\therefore \,\vec E = \dfrac{{{\mu _0}nr}}{2}{I_{\max }}\omega \sin \omega t$
Therefore, The magnitude of the induced electric field inside the solenoid, at a distance $r < R$ from its long central axis is $\dfrac{{{\mu _0}n{I_{\max }}\omega }}{2}r\sin \omega t$ .

Hence, option D is the correct option.

Note: A solenoid has an enameled wire wound which is in the form of a helix.
Therefore, we can say that a solenoid is a hollow pipe on which winding or wires is done.For an ideal solenoid in which the turns are tightly packed and their number is very large, the magnetic field at a point outside the solenoid is zero whereas the electric field is induced both inside and outside the solenoid. The induced electric field outside the solenoid will be conservative in nature which means that $curl(E) = 0$ .