Question

The magnitude of $i$ ampere units is

Answer 1

Divide the given circuit into loops divided by the central wire constituting two resistors. Apply Kirchhoff’s voltage law to these two loops and derive the equations in terms of currents. Also, use the equation for Kirchhoff’s current law to the whole loop and solve the equation obtained to determine the current in the circuit.

Complete step by step answer:
Divide the above given circuit into two loops such as upper loop and lower loop.The current of 1 A gets divided into three branches of the circuit as $i$, ${i_1}$ and ${i_2}$. Draw the given circuit showing the currents in three branches of the circuit.

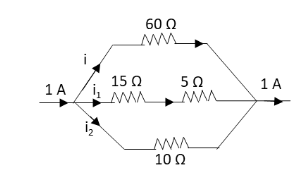
Apply Kirchhoff’s current law to the above circuit.
$i + {i_1} + {i_2} = 1\,{\text{A}}$ …… (1)
Apply Kirchhoff’s voltage law to the upper loop of the circuit.
$- 60i + 5{i_1} + 15{i_1} = 0$
$\Rightarrow - 60i + 20{i_1} = 0$
$\Rightarrow 20{i_1} = 60i$
$\Rightarrow {i_1} = 3i$

Apply Kirchhoff’s voltage law to the lower loop of the circuit.
$- 10{i_2} + 5{i_1} + 15{i_1} = 0$
$- 10{i_2} + 20{i_1} = 0$
$\Rightarrow {i_2} = 2{i_1}$
Substitute $2{i_1}$ for ${i_2}$ in equation (1).
$i + {i_1} + 2{i_1} = 1\,{\text{A}}$
$\Rightarrow i + 3{i_1} = 1\,{\text{A}}$
Substitute $3i$ for ${i_1}$ in the above equation.
$\Rightarrow i + 3\left( {3i} \right) = 1\,{\text{A}}$
$\Rightarrow 10i = 1\,{\text{A}}$
$\therefore i = 0.1\,{\text{A}}$

Hence, the current $i$ through the circuit is $0.1\,{\text{A}}$.

Additional information:
According to Kirchhoff current law the sum of all the currents flowing into a junction or node is equal to the sum of all the currents coming out of the junction.According to Kirchhoff’s voltage law the sum of all the voltage drops into a loop is equal to zero.

Note: The students should be careful while applying Kirchhoff’s voltage law to the loops in the circuit. The students should always remember that the sign of the voltage term will be positive if the direction of the loop is opposite to the direction of current and negative if the direction of loop is along the direction of the current.