Question

The magnitude of electric force on a $2\mu C$ charge placed at the centre O of two equilateral triangles each of side 10cm as shown in the figure is P. If charge A, B, C, D, E and F are $2\mu C$, $2\mu C$, $2\mu C$, $-2\mu C$, $-2\mu C$ and $-2\mu C$ respectively. Then P is –

  ![](https://www.vedantu.com/question-sets/8d1dae23-cd37-470b-b072-741b13729ea36881366235260926560.png)   

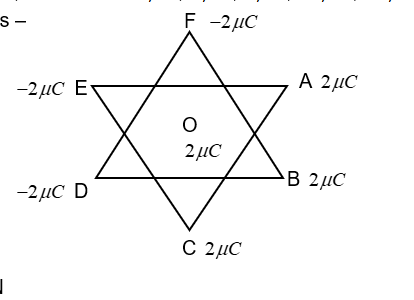
A) 21.6N
B) 64.8N
C) 0
D) 43.2N

Answer 1

We can find the electric force by computing the resultant force on the centre charge at O due to each of the charges placed around it. The vector sum of the electric forces at point O will give the required electric force P acting on the charge at O.

Complete answer:
Let us consider the composition of charges given to us. The charges are placed such that they are at the corners of two equilateral triangles each of side 10cm.

        ![](https://www.vedantu.com/question-sets/04a6419c-1b5a-44e3-af1c-cf6c72aabce61635867326813022541.png)   

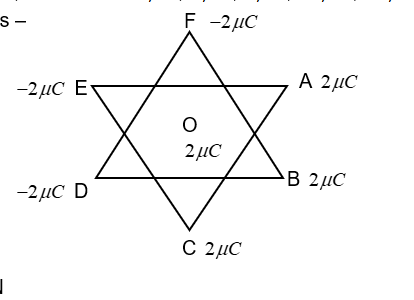
We can find the distance between the centre charge at O to all the other charges at the corners using the given measurements of the sides of the triangle. All the distances OA, OB, OC, OD, OE and OF are equal and let it be ‘r’.

![](https://www.vedantu.com/question-sets/8edaf6df-53c4-4a82-bac5-725c8fae9227304843778895102568.png)   

We can find the distance to all the points from the centre O as –

& r=\dfrac{side}{\sqrt{3}} \\\ & \Rightarrow \text{ }r=\dfrac{10}{\sqrt{3}}cm \\\ \end{aligned}$$ Let us apply the formula for electric force on each charge on the corner as – $$F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$$ We can find the magnitude of the force for all the charge pairs OA, OB, OC, OD, OE and OF using this formula. We know that the force has equal magnitude as all the charges are at equal distance. $$\begin{aligned} & \therefore \text{ }F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}} \\\ & \Rightarrow \text{ }F=9\times {{10}^{9}}\times \dfrac{2\times {{10}^{-6}}\times 2\times {{10}^{-6}}}{{{(\dfrac{10}{\sqrt{3}}\times {{10}^{-2}})}^{2}}} \\\ & \Rightarrow \text{ }F=10.8N\text{ --(1)} \\\ \end{aligned}$$ $$\begin{aligned} & OA=OB=OC=10.8N \\\ & OD=OE=OF=-10.8N \\\ & \therefore \text{ Total force =0N} \\\ \end{aligned}$$ Now, let us consider the direction of force due to two charges on the centre charge O. 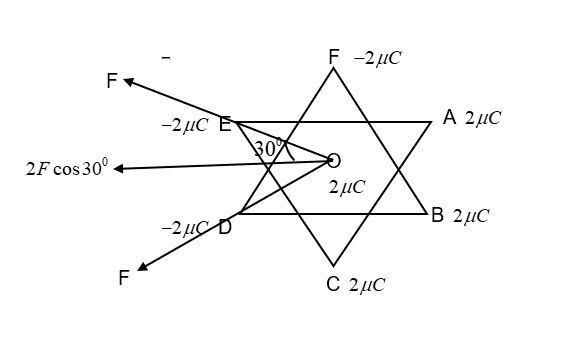 We understand from the above figure that the components of force due to more than one electric charge is present in the system which doesn’t cancel off. Along the -x axis the force F due to E, D and A, B act along. The magnitude of the force component along the -x axis becomes $$4F\cos {{30}^{0}}$$. Now, when two opposite charges act together as in F, A and D. C, we get – Along the +y axis the force is $$2F\sin {{30}^{0}}$$. 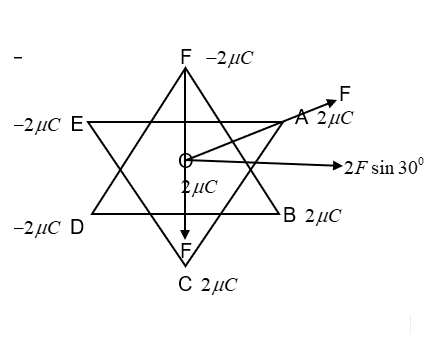 When we consider the C and D we get the same in the opposite direction, as a result it cancels off. But we have the opposite charges at A, E and D, B which gives a 2F magnitude along +y axis. Now, we have two forces along the -x axis and +y axis, which can be added vectorially as – $$\begin{aligned} & {{F}_{r}}=\sqrt{{{(4F\cos {{30}^{0}})}^{2}}+4{{F}^{2}}-2.4F.4F\cos {{90}^{0}}} \\\ & {{F}_{r}}=\sqrt{16{{F}^{2}}\dfrac{3}{4}+4{{F}^{2}}} \\\ & {{F}_{r}}=\sqrt{16{{F}^{2}}} \\\ & {{F}_{r}}=4F \\\ \end{aligned}$$ From (1), $$\begin{aligned} & F=10.8N \\\ & \Rightarrow \text{ }{{F}_{r}}=4\times 10.8 \\\ & \therefore \text{ }{{F}_{r}}=43.2N \\\ \end{aligned}$$ The electric force on the charge at center O is 43.2N **So, the correct answer is “Option D”.** **Note:** The electric force tends to look zero when we just consider the relation between each of the charges on the vertex with the centre charge. But there is interaction between these charges on the vertex and they too contribute to the force on the central charge.