Question
Question: The magnitude of component of vector A = $3\hat{i} + 4\hat{j}$ along vector $2\hat{i} + \hat{j}$ is ...
The magnitude of component of vector A = 3i^+4j^ along vector 2i^+j^ is α. Then find the value of 4α2.
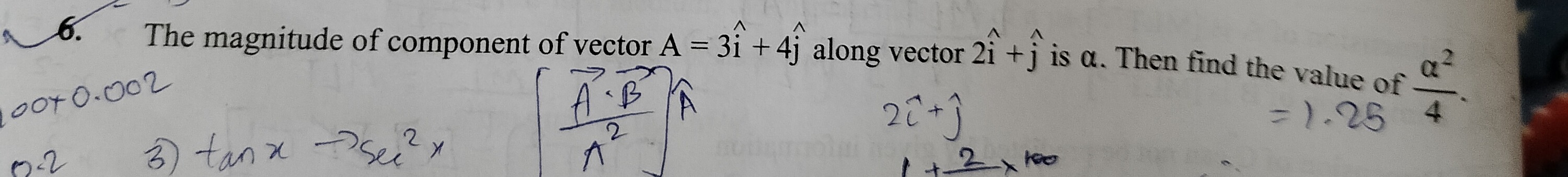
Answer
5
Explanation
Solution
Let A=3i^+4j^ and B=2i^+j^.
The magnitude of the component of vector A along vector B is given by the scalar projection of A onto B, which is α=∣B∣A⋅B.
First, calculate the dot product A⋅B: A⋅B=(3)(2)+(4)(1)=6+4=10.
Next, calculate the magnitude of vector B: ∣B∣=22+12=4+1=5.
Now, calculate the value of α: α=510.
We are asked to find the value of 4α2. Calculate α2: α2=(510)2=(5)2102=5100=20.
Finally, calculate 4α2: 4α2=420=5.
The value of 4α2 is 5.
