Question
Question: The magnetic flux through loop is shown in the fig. It increases according to the relation\({{\phi }...
The magnetic flux through loop is shown in the fig. It increases according to the relationϕB=6t2+7t, where ϕB is in milliwebers and t is in seconds.
(a). What is the magnitude of the emf induced in the loop when t=2s.
(b). What is the direction of current through R?
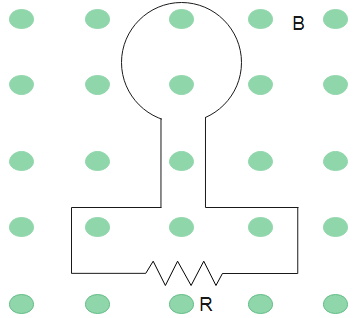
Solution
Given, a loop is kept in a magnetic field such that the flux through it is changing by the given relation. The negative rate of change of magnetic flux is equal to the emf induced. The rate can be calculated by differentiating the change in flux with respect to time. The right hand rule represents the right hand rule.
Formulas used:
e=−dtdϕ
Complete step by step answer:
Given, magnetic flux varies according to the relation ϕB=6t2+7t.
When the magnetic flux through a fixed area varies continuously, an emf is induced. The rate of change of magnetic flux is equal to the emf induced. Therefore,
e=−dtdϕ
Here, e is the emf induced
dtdϕ is represented by the rate of change of flux
ϕB=6t2+7t
We differentiate the above equation with respect to time to get,
dtdϕB=6(2t)+7⇒dtdϕB=12t+7
When t=2s, substituting in the above equation, we get,
e=−dtdϕB=−(12×2+7)⇒e=−31V
Therefore, the emf induced in the loop is −31V.
The right hand rule is used to determine the direction of current in the loop. According to the right hand rule the fingers are curled in the direction of magnetic field then the thumb gives the direction of current. Therefore, the direction of current is shown in the figure below.
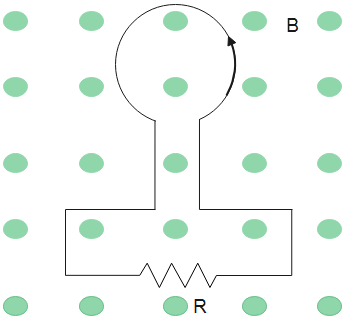
Therefore, the emf induced in the loop is −31V and the direction of current is anticlockwise.
Note: The negative sign in the emf indicates that the emf induced is opposite to the direction of change in flux. This is in accordance with the law of conservation of energy. The current in the loop depends on the emf induced and the resistance in the circuit. The flux can be changed by either moving the loop in a uniform magnetic field or by continuously changing the magnetic field. Dot means that the direction of the magnetic field is in the plane of the paper.
