Question

The magnetic field in the plane electromagnetic wave is given by $1.5 \times 10^{-8} \sin(0.5 \times 10^3 x + 10^{11} t)$ Tesla. Which of the following options is correct?

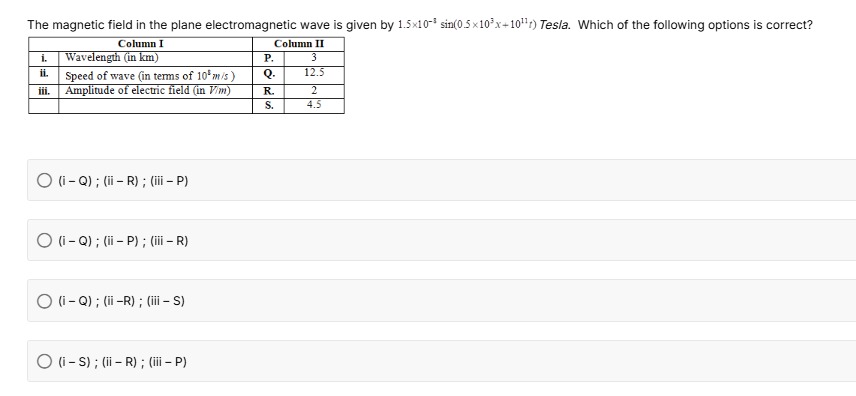
• A. (i - Q); (ii - R); (iii - P)
• B. (i - Q); (ii - P); (iii - R)
• C. (i - Q); (ii - R); (iii - S)
• D. (i - S); (ii - R); (iii - P)

Answer 1

Answer: (A)

(i - Q); (ii - R); (iii - P)

Answer 2

The magnetic field equation is given by $B = 1.5 \times 10^{-8} \sin(0.5 \times 10^3 x + 10^{11} t)$ Tesla. Comparing with the standard form $B = B_0 \sin(kx + \omega t)$:

• Amplitude of magnetic field, $B_0 = 1.5 \times 10^{-8}$ T.
• Wave number, $k = 0.5 \times 10^3 \text{ rad/m} = 500 \text{ rad/m}$.
• Angular frequency, $\omega = 10^{11} \text{ rad/s}$.

ii. Speed of wave (in terms of $10^8$ m/s): The speed of an electromagnetic wave is $v = \frac{\omega}{k}$. $v = \frac{10^{11} \text{ rad/s}}{500 \text{ rad/m}} = \frac{10^{11}}{5 \times 10^2} \text{ m/s} = 0.2 \times 10^9 \text{ m/s} = 2 \times 10^8 \text{ m/s}$. This matches option R (2).

iii. Amplitude of electric field (in V/m): The amplitude of the electric field ($E_0$) is related to the amplitude of the magnetic field ($B_0$) by $E_0 = v B_0$. $E_0 = (2 \times 10^8 \text{ m/s}) \times (1.5 \times 10^{-8} \text{ T}) = 3 \text{ V/m}$. This matches option P (3).

i. Wavelength (in km): The wavelength ($\lambda$) is related to the wave number ($k$) by $k = \frac{2\pi}{\lambda}$. $\lambda = \frac{2\pi}{k} = \frac{2\pi}{500 \text{ rad/m}} = \frac{\pi}{250} \text{ m}$. Converting to kilometers: $\lambda = \frac{\pi}{250} \text{ m} = \frac{\pi}{250 \times 1000} \text{ km} = \frac{\pi}{250000} \text{ km}$. Using $\pi \approx 3.14159$, $\lambda \approx 0.000012566 \text{ km} = 1.2566 \times 10^{-5} \text{ km}$. This calculated wavelength does not directly match any of the options in Column II (3, 12.5, 2, 4.5 km). However, if we assume there might be a typo in the question and $k$ was intended to be $0.5 \times 10^{-3}$ for the wavelength calculation, then: $\lambda = \frac{2\pi}{0.5 \times 10^{-3}} = \frac{2\pi}{5 \times 10^{-4}} = 0.4\pi \times 10^4 \text{ m} = 4000\pi \text{ m} \approx 12566 \text{ m} = 12.566 \text{ km}$. This value closely matches option Q (12.5 km).

Given that (ii - R) and (iii - P) are definitively calculated, and assuming one of the options must be correct, the option that includes (i - Q) is the most plausible choice, suggesting a potential typo in the original question's wave number for the wavelength calculation.

Therefore, the correct option is (i - Q); (ii - R); (iii - P).