Question

The magnetic field existing in a region is given by $\overrightarrow B = {B_o}\left[ {1 + \dfrac{x}{l}} \right]\hat k$ . A square loop of edge $l$ and carrying current $I$ is placed with its edges parallel to the x -y axis. The magnitude of the net magnetic force experienced by the loop is:
A. $2{B_o}Il$
B. $3{B_o}Il$
C. ${B_o}Il$
D. Zero

Answer 1

In this question, we need to determine the magnitude of the net magnetic force experienced by the loop such that magnetic field existing in a region is given by $\overrightarrow B = {B_o}\left[ {1 + \dfrac{x}{l}} \right]\hat k$. For this, we will find the force on all four edges separately and then, add them. Two of the sides need integration. But with simple logic, one can eliminate two expressions.

Complete step by step solution:
The diagram for the above question can be drawn as

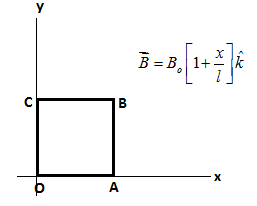
For simplicity we can demote one corner as shown as before.
Let the current flows counterclockwise
Here the main catch is that the magnetic field depends on the distance from the x axis.
So there is a varying magnetic field in sides OA and BC. But see that the direction of current is opposite in both the arms. Other than these the length and magnetic field parameters are the same. Hence the force will come up to be equal and opposite. Thus, the force in these arms will cancel.
So there is only two arms left
For BC,

$$x = l \\\ \overrightarrow B = 2{B_o}\hat k \\\$$

Now the force given by

$$F = ilB \\\ \Rightarrow F = 2Il{B_o} \\\$$

Similarly, for CO,

$$x = 0 \\\ \overrightarrow B = {B_o}\hat k \\\$$

Now the force given by

$$F = ilB \\\ \Rightarrow F = Il{B_o} \\\$$

Since the current in both the arms is opposite the forces are opposite
Hence the net force is given by

$$F = 2Il{B_o} - Il{B_o} \\\ = Il{B_o} \\\$$

So, the correct answer is “Option C”.

Note:
It is important to note here that as the same current is flowing in the opposite direction of the arms of the loop so, we have subtracted the forces acting on the arms due to current to evaluate the net force on the loop. One needs good knowledge to solve these types of questions. Also, one needs to apply some logic to eliminate the like terms but opposite signs.