Question

The magnetic field existing in a region is given by-
$\vec B = {B_0}\left( {1 + \dfrac{x}{l}} \right)\hat k.$
A square loop of edge l and carrying a current i, is placed with its edges parallel to the X-Y axes. Find the magnitude of the net magnetic force experienced by the loop.

Answer 1

- Hint: First, we will draw a figure supporting the conditions given by the question. Then we will find out the force exerted on each side of the square loop by using the suitable formula. Then we will add the magnitude of these forces together to get the desired answer. Refer to the solution below.

Formula used: $F = iBl$, $\left| {{F_{net}}} \right| = {F_1} + {F_2} + {F_3} + {F_4}$.

Complete step-by-step solution -

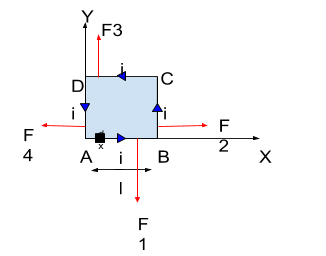
From the given magnetic field, it is clear that its direction is in Z direction.
The magnetic field is-
$\Rightarrow \vec B = {B_0}\left( {1 + \dfrac{x}{l}} \right)\hat k.$
Now, we will find out the force and its direction acting on the loop.
Force due to a current carrying wire is calculated by-
$\Rightarrow F = iBl$
Force $\left( {{F_1}} \right)$ due to the side AB of the square will be-
Let’s assume a small element on the side AB of the square. Let the length of that element be dx.
$\Rightarrow d{F_1} = iBdx$
Integrating both sides, we will get (the limit will be from 0 to $l$ since the point A is on origin and the length of the sides of the square is given as $l$)-
$\Rightarrow \int {d{F_1} = \int\limits_0^l {iBdx} } \\\ \\\ \Rightarrow {F_1} = \int\limits_0^l {i{B_0}\left( {1 + \dfrac{x}{l}} \right)} dx \\\ \\\ \Rightarrow {F_1} = \int\limits_0^l {i{B_0}dx + \int\limits_0^l {i{B_0}\dfrac{x}{l}dx} } \\\ \\\ \Rightarrow {F_1} = i{B_0}\left[ x \right]_0^l + \dfrac{{i{B_0}}}{l}\left[ {\dfrac{{{x^2}}}{2}} \right]_0^l \\\ \\\ \Rightarrow {F_1} = i{B_0}l + \dfrac{{i{B_0}l}}{l} \times \dfrac{{{l^2}}}{2} \\\ \\\ \Rightarrow {F_1} = i{B_0}l + \dfrac{{i{B_0}l}}{2} \\\ \\\ \Rightarrow {F_1} = \dfrac{3}{2}i{B_0}l \\\$
Now, using Fleming’s right hand rule on the side AB, we know that the direction of the force will be downwards.
As we can see from the figure, sides AB and CD are parallel to each other. Only the direction changes. Thus-
$\Rightarrow {F_3} = \dfrac{3}{2}i{B_0}l$
And the direction of the force according to Fleming's rule will be upwards.
Side DA of the square is on the Y-axis. And we know that the X coordinate on Y-axis is always 0.
The value of magnetic field is given as-
$\Rightarrow B = {B_0}\left( {1 + \dfrac{x}{l}} \right)$
Putting the value of x as 0, we get-
$\Rightarrow B = {B_0}\left( {1 + \dfrac{x}{l}} \right) \\\ \\\ \Rightarrow B = {B_0}\left( {1 + \dfrac{0}{l}} \right) \\\ \\\ \Rightarrow B = {B_0}\left( {1 + \dfrac{x}{l}} \right) \\\ \\\ \Rightarrow B = {B_0} \\\$
Hence, the value of force on the side DA of the square will be-
$\Rightarrow {F_4} = iBl \\\ \\\ \Rightarrow {F_4} = i{B_0}l \\\$
Now, using Fleming’s right hand rule on the side DA, we know that the direction of the force will be on the left.
Similarly, we will calculate the value of ${F_2}$ for the side CB.
The value of x will be $l$ (since the distance of the point B from the origin is $l$).
The value of magnetic field is given as-
$\Rightarrow B = {B_0}\left( {1 + \dfrac{x}{l}} \right)$
Putting the value of x as $l$, we get-
$\Rightarrow B = {B_0}\left( {1 + \dfrac{x}{l}} \right) \\\ \\\ \Rightarrow B = {B_0}\left( {1 + \dfrac{l}{l}} \right) \\\ \\\ \Rightarrow B = {B_0}\left( {1 + 1} \right) \\\ \\\ \Rightarrow B = 2{B_0} \\\$
Hence, the value of force on the side CB of the square will be-
$\Rightarrow {F_2} = iBl \\\ \\\ \Rightarrow {F_2} = 2i{B_0}l \\\$
Now, using Fleming’s right hand rule on the side CB, we know that the direction of the force will be on the right.
Now, the net magnetic force experienced by the square loop will be-
$\Rightarrow \left| {{F_{net}}} \right| = {F_1} + {F_2} + {F_3} + {F_4}$
As we can see from the above calculations, the magnitude of the force ${F_1}$ and ${F_3}$ are equal to each other in magnitude but the directions are opposite to each other. So, they will cancel each other out. The left force is ${F_2}$ and ${F_4}$. Thus-
$\Rightarrow \left| {{F_{net}}} \right| = \dfrac{3}{2}i{B_0}l + 2i{B_0}l - \dfrac{3}{2}i{B_0}l - i{B_0}l \\\ \\\ \Rightarrow \left| {{F_{net}}} \right| = i{B_0}l \\\$

Note: Magnetic force, attraction or repulsion arises between particles which are electrically charged due to the motion. The magnetic force between two moving charges can be represented as the effect exerted on either of the charges due to a magnetic field produced by another charge.