Question

The magnetic field existing in a region is given by $\overrightarrow{B}={{B}_{\circ }}\left( 1+\dfrac{x}{l} \right)\widehat{k}$ . A square loop of edge $l$ and carrying current $i$ is placed with its edge parallel to the XY axes. Find the magnitude of the net magnetic force experienced by the loop.
a)$\dfrac{1}{2}l{{B}_{\circ }}i$
b)Zero
c)$i{{B}_{\circ }}l$
d)$2i{{B}_{\circ }}l$

Answer 1

To determine the net force on the loop we should first obtain the individual force on each edge of the loop. Once can find the force on the edges of the loop using the expression of force on a current carrying conductor. Further we can accordingly obtain the net force on the loop by considering the direction of the action of force on each of the edges.
Formula used:
$\overrightarrow{F}=il\overrightarrow{B}$

Complete answer:

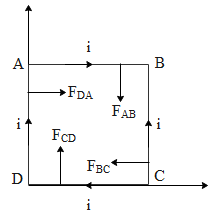
In the above figure we can see that the coil ABCD is placed as shown carrying current ‘i’. The forces on the respective edges are also shown in the above figure using the right hand thumb rule. From the question it can be clearly seen that the magnetic field is a function of x. Hence the net magnetic field on the edges of the loop i.e. DC and AB will have the same net magnetic field. If a wire of length ‘l’ carries a current ‘i’, such that such that the magnetic field is perpendicular to the direction of the current then the force on the wire due to magnetic field is given by,
$\overrightarrow{F}=il\overrightarrow{B}$
The force on the coil AB and DC are equal and opposite in direction. They are equal as they have the same length and placed in the same magnetic field and carry the same current but the flow is in the opposite direction. Therefore they will cancel out each other.
The force on the wire AD and BC are also opposite in direction. The force on the section AD is equal to,
$\begin{aligned} & {{\overrightarrow{F}}_{AD}}=il\overrightarrow{B} \\\ & {{\overrightarrow{F}}_{AD}}=il{{B}_{\circ }}\left( 1+\dfrac{x}{l} \right),\ x=0\to AD \\\ & {{\overrightarrow{F}}_{AD}}=il{{B}_{\circ }}\left( 1+\dfrac{0}{l} \right)=il{{B}_{\circ }} \\\ \end{aligned}$
Similarly the force on the section BC is equal to,
$\begin{aligned} & {{\overrightarrow{F}}_{BC}}=il\overrightarrow{B} \\\ & {{\overrightarrow{F}}_{BC}}=il{{B}_{\circ }}\left( 1+\dfrac{l}{l} \right),\ x=l\to BC \\\ & {{\overrightarrow{F}}_{BC}}=il{{B}_{\circ }}\left( 2 \right)=2il{{B}_{\circ }} \\\ \end{aligned}$
Hence the net force (F) on the loop is equal to,
$\begin{aligned} & F={{F}_{AB}}+{{F}_{BC}}+{{F}_{CD}}+{{F}_{DA}},\text{ }\left| {{F}_{AB}} \right|=-\left| {{F}_{CD}} \right| \\\ & \Rightarrow F={{F}_{BC}}+{{F}_{DA}} \\\ \end{aligned}$
Similarly the forces on the section AD and BC are in the opposite direction but have different magnitudes. Hence,
$\begin{aligned} & F={{F}_{BC}}-{{F}_{DA}} \\\ & \Rightarrow F=2il{{B}_{\circ }}-il{{B}_{\circ }}=il{{B}_{\circ }} \\\ \end{aligned}$

Therefore the correct answer of the above question is option c.

Note:
The right hand thumb rule states that if the middle finger indicates the direction of the magnetic field, the fore finger indicates the direction of the current then the thumb indicates the direction of the force on the wire given that all the three fingers are mutually perpendicular to each other. It is also to be noted that the force can also be obtained mathematically by considering the respective cross product between the field and the current element.