Solveeit Logo
Login

Question

Question: The magnetic field \(dB\) at a point r meter always from the current element \(Id\vec l\)aligned at ...

The magnetic field dBdB at a point r meter always from the current element Idl⃗Id\vec laligned at angle of the θ\theta with respect to the current element is-
A) (μ04π)(Idl⃗sin⁡θr)\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l\sin \theta }}{r}} \right)
B) (μ04π)(Idl⃗r2)\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l}}{{{r^2}}}} \right)
C) (μ04π)(Idl⃗sin⁡θr2)\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}} \right)
D) (μ04π)(Idl⃗r)\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l}}{{{r^{}}}}} \right)

Explanation

Solution

Hint
It can be answered with the help of the Biot savart law, because this law gives the value of the dBdB with the current element Idl⃗Id\vec l.

Complete answer:
According to the biot savart law-

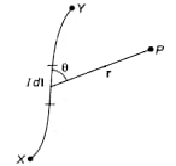
The magnetic field due the small length dldlin which the I current flowing the conductor
Then
dB∝IdB \propto I(current flowing in the conductor)
dB∝dldB \propto dl (small length)
dB∝1r2dB \propto \dfrac{1}{{{r^2}}} (inverse of the square of the distance of point p from thedldl)
And dBdBα sin⁡θ\sin \theta (sine of the angle made by the dldl with point p)
Hence we can say that
dB∝Idl⃗sin⁡θr2dB \propto \dfrac{{Id\vec l\sin \theta }}{{{r^2}}}
Or it can be also written as
dBdB = KIdl⃗sin⁡θr2K\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}
Where proportionality constant is equal to the μ04π\dfrac{{{\mu _0}}}{{4\pi }}
Or numerically it can be written as
K=μ04πK = \dfrac{{{\mu _0}}}{{4\pi }}
Hence the biot savart law
dBdB = (μ04π)(Idl⃗sin⁡θr2)\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}} \right)
The final answer is given by
dBdB = (μ04π)(Idl⃗sin⁡θr2)\left( {\dfrac{{{\mu _0}}}{{4\pi }}} \right)\left( {\dfrac{{Id\vec l\sin \theta }}{{{r^2}}}} \right).
Option (C) is the correct answer.

Note
This law was given by the two scientist biot and savart, they both were two different scientists who gave the value of the dBdB. The magnetic concept was firstly realized by the Oesterd's; he noticed that the needle of the magnet moved when current was passing from the wire nearer to it. He gave certain ways to find the direction of the magnetic field like a swimmer's rule.