Question
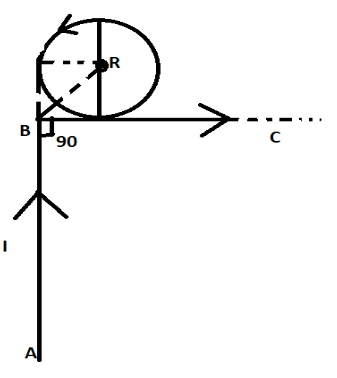
Question: The magnetic field at the center of the circular loop as shown in the figure, when the single wire i...
The magnetic field at the center of the circular loop as shown in the figure, when the single wire is bent to form a circular loop and also extends to form a straight section is:
A. 2Rμ0I⊙
B. 2Rμ0I(1+π21)⊙
C. 2Rμ0I(1−π21)⊗
D. Rμ0I(1−π21)⊗
Solution
In the above question, we have to find the total magnetic field. Then firstly, finding the magnetic field along the straight wire and then extending the circular loop and then again, the magnetic field of the straight wire. After adding all the magnetic fields, we got the final answer.
Complete step by step answer:
The total magnetic field will be given by adding the magnetic field of straight line and the magnetic field of the circular loop and again the magnetic field of straight line.Magnetic field can be calculated by the Biot savart’s law whose expression be given by,
dB=4πμ0r3Idr×r
Magnetic field of straight wire be given by the formula,
B=4πrμ0I(sinθ1+sinθ2)
where θ1,θ2 are the angles corresponding to the two ends of the wire.
Now, the magnetic field along AB,
B1=4πRμ0I(sin2π−sin4π)⊗ ⇒B1=4πRμ0I(1−21)⊗ ……(1)
Now, the magnetic field along the circular loop
B2=2Rμ0I⊙ ……(2)
Magnetic field along the wire BC,
B3=4πRμ0I(sin2π+sin4π)⊙ ⇒B3=4πRμ0I(1+21)⊙ ……(3)
Now adding all the above marked equations:
B=B1+B2+B3
\Rightarrow\overrightarrow B = \left( {\dfrac{{{\mu _0}I}}{{2R}} + \dfrac{{2{\mu _0}I}}{{4\pi R}}\dfrac{1}{{\sqrt 2 }}} \right) \odot \\\
\therefore\overrightarrow B = \dfrac{{{\mu _0}I}}{{2R}}\left( {1 + \dfrac{1}{{\pi \sqrt 2 }}} \right) \odot \\\
Hence, the correct option is B.
Note: The value of proportionality is 4πμ0=10−7NA−2.Biot savart law is a vector quantity which contains both magnitude and direction.⊗ is the inward direction of the field and ⊙ is the outward direction of the field.
