Question

The machine as shown has $2$ rods of length $1m$ connected by a pivot at the top. The end of one rod is connected to the floor by a stationary pivot and the end of the other rod has a roller that rolls along the floor in a slot. As the roller goes back and forth, a $2kg$ weight moves up and down. If the roller is moving towards right at a constant speed, the weight moves up with a:

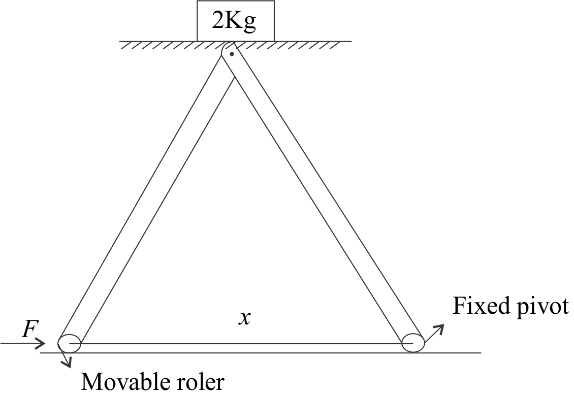
(A) Constant speed
(B) Increasing speed which is $\dfrac{3}{4}th$ of the
(C) Roller when weight is $0.4m$ above the ground
(D) Decreasing speed

Answer 1

Hint From the given diagram we can understand the question the weight is moving up and down and the roller is moving left. We have to find the speed of the weight moving up. By differentiating the distance covered by the weight we will get the speed of the weight since speed (velocity) is the change in displacement with respect to time.

Complete step by step answer
We know that the velocity is the rate of change in displacement, s with respect to time, t.
Here from the diagram we can see that the weight moves up by covering the distance y in time t towards the point C.
Let ${V_c}$ be the speed (velocity) of the weight moving up towards the point C.
Then, rate of change in y with respect to time is the speed of weight moving up
$\Rightarrow \dfrac{{dy}}{{dt}} = {V_c}{\text{ }} \to {\text{1}}$
${V_c}$ is the velocity (speed) of the moving up toward point C
Let ${V_A}$ be the velocity (speed) with which the roller moves right, then
$\Rightarrow \dfrac{{dx}}{{dt}} = {V_A}{\text{ }} \to 2$
${V_A}$ is the velocity (speed) of the moving right
We can understand clearly if we see the diagram

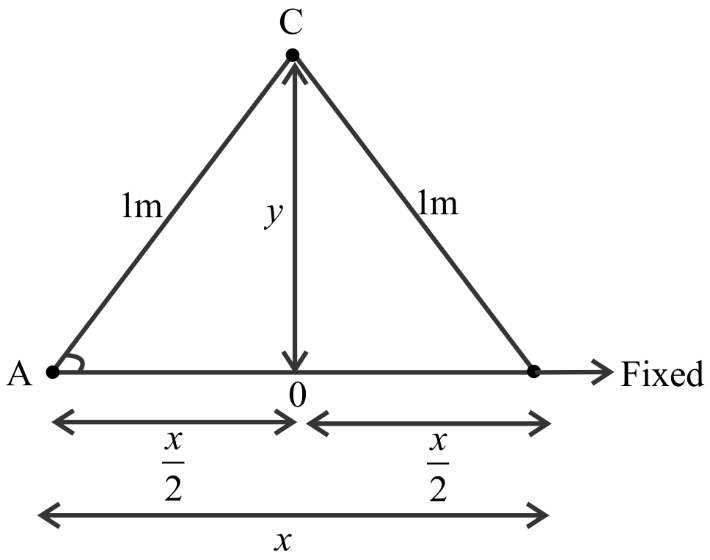
From the diagram,
Let us take the triangle AOC, then
$\Rightarrow \sin \theta = \dfrac{{{\text{opposite side}}}}{{hypotenuse}}$
$\Rightarrow \sin \theta = \dfrac{y}{1}$
$\Rightarrow \sin \theta = y$
Differentiating above equation,
$\Rightarrow \sin \theta \dfrac{{d\theta }}{{dt}} = \dfrac{{dy}}{{dt}}$
From equation 2 we get
$\Rightarrow \sin \theta \dfrac{{d\theta }}{{dt}} = {V_C}$
$\Rightarrow \dfrac{{d\theta }}{{dt}} = \dfrac{{{V_c}}}{{\sin \theta }}{\text{ }} \to 3$
Then,
We know that,
$\Rightarrow \cos \theta = \dfrac{{{\text{adjacent side}}}}{{{\text{hypotenuse}}}}$
$\Rightarrow \cos \theta = \dfrac{{\dfrac{x}{2}}}{1}$
$\Rightarrow \cos \theta = \dfrac{x}{2}$
Differentiating
$\Rightarrow \cos \theta \dfrac{{d\theta }}{{dt}} = \dfrac{{\dfrac{{dx}}{{dt}}}}{2}$
From equation 1 we get
$\Rightarrow - \cos \theta \dfrac{{d\theta }}{{dt}} = \dfrac{{{V_A}}}{2}$
$\Rightarrow \dfrac{{d\theta }}{{dt}} = - \dfrac{{{V_A}}}{{2\cos \theta }}{\text{ }} \to {\text{4}}$
From the equation 3 and 4 we get
$\Rightarrow \dfrac{{{V_C}}}{{\sin \theta }} = \dfrac{{{V_A}}}{{2\cos \theta }}$
$\Rightarrow {V_c} = \dfrac{{{V_A}}}{{2\tan \theta }}$
It is given that the roller is moving right, if the roller moves rightwards then the angle $\theta$ increases, if $\theta$ increases then ${V_C}$ will decrease (from the above relation)
${V_c}$ is the speed (velocity) of the weight moving up towards the point C.
So, the speed decreases when the weight moves upward.

Hence the correct answer is option (D) decreasing speed

Note We are saying that if $\theta$ increases then ${V_C}$ will decrease from the relation we got
$\Rightarrow {V_c} = \dfrac{{{V_A}}}{{2\tan \theta }}$
We can see that ${V_C}$ is directly proportional to ${V_A}$ and inversely proportional to $\theta$, so if the $\theta$ increases then ${V_C}$ will decrease.