Question

The M.I. of a semi-circular ring of mass M and radius R about an axis lying on the plane which is passing through its center and with an angle $\theta$ with the line joining its end is –

& \text{A) }\dfrac{M{{R}^{2}}}{2}\text{, if }\theta ={{0}^{0}} \\\ & \text{B) }\dfrac{M{{R}^{2}}}{2}\text{, if }\theta ={{60}^{0}} \\\ & \text{C) }\dfrac{M{{R}^{2}}}{2}\text{, if }\theta ={{120}^{0}} \\\ & \text{D) }\dfrac{M{{R}^{2}}}{2}\text{, if }\theta ={{180}^{0}} \\\ \end{aligned}$$

Answer 1

We need to understand the concept of moment of inertia and its dependence on the different planes or axes of the body under consideration. These ideas are required to solve the given problem and find the required moment of inertia.

Complete answer:
The moment of inertia is considered as the rotational analogue of the mass. The mass of the body which causes the effect of rotation in the system is dependent on its axis of rotation and is different along each axis unlike the uniform motion which has a constant mass along any direction. The moment of inertia of the body in the particular axis is important to understand the dynamics of the system in the rotational motion.

In the given situation, a semi-circular ring is considered which has a random axis which is introduced such that it is lying on the plane that passes through the center and with an angle with its diameter.

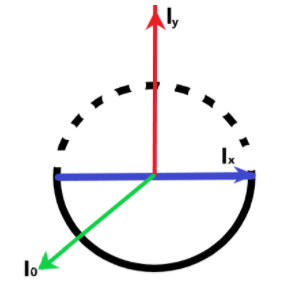
For a circular ring, the moment of inertia through an axis which is perpendicular to the plane through the center is given as –
${{I}_{0}}=M{{R}^{2}}$

Now, we can apply the perpendicular axes theorem in order to obtain the moment of inertia of the circular ring along the diameter as –

& {{I}_{0}}={{I}_{x}}+{{I}_{y}} \\\ & \text{but, }{{\text{I}}_{x}}={{I}_{y}} \\\ & \Rightarrow M{{R}^{2}}=2I \\\ & \therefore I=\dfrac{M{{R}^{2}}}{2} \\\ \end{aligned}$$ This is situation is possible only when the angle between the diameter and the axis under consideration is zero. **So, the correct answer is option A.** **Note:** The perpendicular axes theorem states that the sum of the moment of inertia of two axes which are mutually perpendicular to each other will give the moment of inertia of the third axis which is perpendicular to both of the initial axes as we have here.