Question
Question: The log-log graph between the energy \( E \) of an electron and its de-Broglie wavelength \( \lambda...
The log-log graph between the energy E of an electron and its de-Broglie wavelength λ will be:
(A) 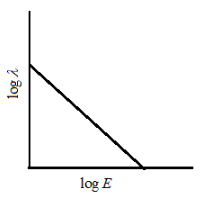
(B) 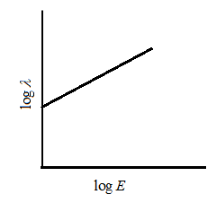
(C) 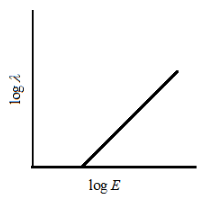
(D) 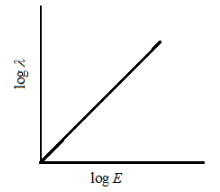
Solution
Here, the log-log graph between energy and wavelength is given. First of all, we must know the relation between energy and wavelength, from that we van be able to calculate the equation of these lines shown in graphs and if the equation matches one of the lines then that would be our answer.
Complete Step By Step Answer:
Here, we have to use the wavelength and momentum relation first so that we could be able to find the wavelength and then the energy relation would be used as below:
λ -Wavelength, E -energy and they are given as:
λ=mvh …. (1)
E=21mv2
The above equation can also be written as:
⇒E=2m1m2v2
⇒2mE=m2v2
⇒mv=2mE
Putting the value of mv from above equation in equation (1)
Therefore, we get
⇒λ=2mEh …. (2)
Thus we have obtained the energy wavelength relationship.
Now, taking log on both sides of equation (2)
We get,
⇒logλ=log2mEh
⇒logλ=log2mh+logE1 …. ( ∵logmn=logm+logn )
⇒logλ=log2mh−21logE …. ( ∵logE21=21logE )
Here, log2mh will be constant and 21logE would be the varying quantity
Thus, on rearranging the above equation, we get
⇒logλ=−21logE+log2mh ….. (3)
Now, let us compare this equation with straight line equation y=mx+c , we get
That, equation (3) gives
m=−21
Here, in the options all contain straight lines but we have to identify whether their slopes are positive or negative.
Option A - straight line and negative slope
Option B - straight line and positive slope
Option C - straight line and positive slope
Option D - straight line and positive slope
Hence, the correct answer is option A.
Note:
Here, we need to derive the energy-wavelength relationship and carry out the procedure. We here used the laws of indices as well as the law of logs. We must know these concepts to solve these types of problems. In the above solution it has been mentioned which laws we are using. At last we used the straight line equation and compared it with the answer we have derived and it led us to the answer.
