Question

The locus of z, for $\arg \,z\, = \dfrac{{ - \pi }}{3}$ is
(A). Same as the locus of z for $\arg \,\,z\, = \dfrac{{2\pi }}{3}$
(B). Same as the locus of z for $\arg \,\,z\, = \dfrac{\pi }{3}$
(C). The part of the straight line $\sqrt 3 x + y = 0$ with $\left( {y < 0,x > 0} \right)$
(D). The part of the straight line $\sqrt 3 x + y = 0$ with $\left( {y > 0,x < 0} \right)$

Answer 1

Hint: Assume z (complex number) with some variables. Now, substitute it into the condition given in the question. Now plot the graph with the given argument. Convert the arg into terms of ${\tan ^{ - 1}}$. Now get the relation between x,y by applying general trigonometry knowledge. This relation of x,y is called the locus of z. Now check with all options one by one.

Complete step-by-step solution -
Given condition in the question, can be written as the form:
Z is a complex number with $\arg \,z\, = \dfrac{{ - \pi }}{3}$.
Let us assume the number z to be $x + iy$. Plotting $\theta = \dfrac{\pi }{3}$ graph we get:

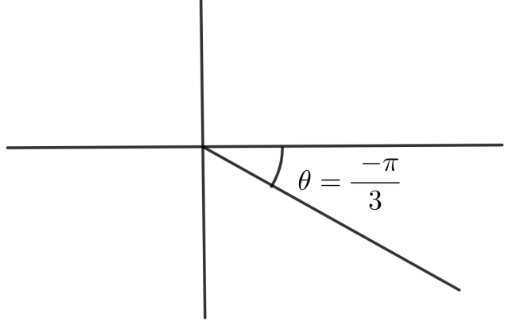
By basic knowledge of complex number we can say that:
$\arg \,z\, = ta{n^{ - 1}}\left( {\dfrac{{imaginary\,\,part}}{{real\,\,part}}} \right)$
By substituting our assumed z into this equation, we get it as:
$Ta{n^{ - 1}}\left( {\dfrac{y}{x}} \right) = \dfrac{{ - \pi }}{3}$
By applying tan on both sides of equation, we get it as:
$tan\left[ {ta{n^{ - 1}}\left( {\dfrac{y}{x}} \right)} \right] = tan\left( {\dfrac{{ - \pi }}{3}} \right)$
By simplifying the term on left side, we get it as:
$tan\left[ {ta{n^{ - 1}}\left( {\dfrac{y}{x}} \right)} \right] = - \sqrt 3$
By simplifying the term of right side, we get it as:
$\dfrac{y}{x} = - \sqrt 3$
By multiplying with x on both sides, we get it as:
$y = - \sqrt 3 x$
The locus given in option (a) can be written as:
Locus of $\arg \,\,z\, = \dfrac{{2\pi }}{3} = \pi + \dfrac{\pi }{3}$ ,
By using formula of arg, we can say it as follows:
$Ta{n^{ - 1}}\left( {\dfrac{y}{x}} \right) = \pi + \dfrac{\pi }{3}$
$\Rightarrow \dfrac{y}{x} = tan\left( {\pi + \dfrac{\pi }{3}} \right) = - \sqrt 3$
So, this locus matches with ours. So this is the correct answer.
The locus in option (b) can be written as:
$Ta{n^{ - 1}}\left( {\dfrac{y}{x}} \right) = \dfrac{\pi }{3}$
$\Rightarrow \dfrac{y}{x} = tan\left( {\dfrac{\pi }{3}} \right) = \sqrt 3$
So, this is the wrong option.
The locus in part (c) can be written as:
The part of the straight line $\sqrt 3 x + y = 0$ with $\left( {y < 0,x > 0} \right)$
Our z is in ${4^{th}}$ quadrant i.e, $x > 0,y < 0$. So, this locus is the correct option.
The locus in part (d) can be written as:
The part of the straight line $\sqrt 3 x + y = 0$ with $\left( {y > 0,x < 0} \right)$
$y > 0,x < 0$ is the second quadrant. So, this is the wrong option.
Therefore, option (a) and (c) is correct for the given question.

Note: Be careful in applying the tan of the given angle. The angle must be $\left( {\dfrac{{ - \pi }}{2},\dfrac{\pi }{2}} \right)$. Hence it is in ${4^{th}}$ quadrant. So, you can apply directly. While checking the option (c) and (d) be careful while denoting the quadrant. Generally, students confuse between x,y and give wrong answers.