Question

The locus of the vertices of the family of parabolas $y = \frac{a^3x^2}{3} + \frac{a^2x}{2} - 2a$ is:

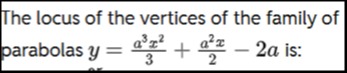
• A. xy = 105/64
• B. xy = 64/105
• C. xy = 35/16
• D. xy = 16/35

Answer 1

Answer: (A)

xy = 105/64

Answer 2

The given equation is $y = \frac{a^3x^2}{3} + \frac{a^2x}{2} - 2a$.

To find the vertex, we differentiate with respect to $x$: $\frac{dy}{dx} = \frac{2a^3x}{3} + \frac{a^2}{2}$.

Setting $\frac{dy}{dx} = 0$: $\frac{2a^3x}{3} + \frac{a^2}{2} = 0$.

Assuming $a \neq 0$, we get $\frac{2ax}{3} = -\frac{1}{2}$, so $a = -\frac{3}{4x}$.

Substitute this back into the original equation: $y = \frac{1}{3}\left(-\frac{3}{4x}\right)^3x^2 + \frac{1}{2}\left(-\frac{3}{4x}\right)^2x - 2\left(-\frac{3}{4x}\right)$ $y = \frac{1}{3}\left(-\frac{27}{64x^3}\right)x^2 + \frac{1}{2}\left(\frac{9}{16x^2}\right)x + \frac{6}{4x}$ $y = -\frac{9}{64x} + \frac{9}{32x} + \frac{3}{2x}$ $y = \frac{-9 + 18 + 96}{64x}$ $y = \frac{105}{64x}$

Thus, the locus is $xy = \frac{105}{64}$.