Question

The locus of the point of intersection of perpendicular straight lines which are at constant distance ‘P’ from the origin is:
A) ${X^2} + {Y^2} = 4{P^2}$
B) ${X^2} + {Y^2} = 3{P^2}$
C) ${X^2} + {Y^2} = 2{P^2}$
D) ${X^2} + {Y^2} = {P^2}$

Answer 1

first of all let the point is (h,k) then find the perpendicular distance from the origin. Thereafter use the foot of perpendicular formula and find the coordinate of (h,k). in final replace (h,k) with (X,Y).

Complete step by step solution:
Given the perpendicular distance from the origin is P
We have to find the locus of the point of intersection of perpendicular straight lines which is at a distance P from the origin.

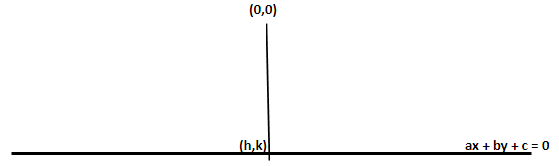
Suppose the point is $(h,k)$and the line is $ax + by + c = 0$ and the perpendicular distance from origin to the line $ax + by + c = 0$ is P
Let find the perpendicular distance P
$P = \dfrac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$
$P = \dfrac{{\left| {a \times 0 + b \times 0 + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$
$P = \dfrac{{\left| c \right|}}{{\sqrt {{a^2} + {b^2}} }}$ ………(i)
Now find the point foot of perpendicular $(h,k)$
By using the formula $\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = - \dfrac{{\left( {a{x_1} + b{y_1} + c} \right)}}{{{a^2} + {b^2}}}$
$\dfrac{{h - 0}}{a} = \dfrac{{k - 0}}{b} = - \dfrac{{\left( {a \times 0 + b \times 0 + c} \right)}}{{{a^2} + {b^2}}}$
$\dfrac{h}{a} = \dfrac{k}{b} = \dfrac{{ - c}}{{{a^2} + {b^2}}}$
$h = \dfrac{{ - ac}}{{{a^2} + {b^2}}}$ ……..(ii)
$k = \dfrac{{ - bc}}{{{a^2} + {b^2}}}$ …….(iii)
Squaring equation (ii) and (iii) and add
We get,
${h^2} = \dfrac{{{a^2}{c^2}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}}$
${k^2} = \dfrac{{{b^2}{c^2}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}}$
${h^2} + {k^2} = \dfrac{{{a^2}{c^2}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}} + \dfrac{{{b^2}{c^2}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}}$
Take ${c^2}$ common
We get,
${h^2} + {k^2} = \dfrac{{{c^2}\left( {{a^2} + {b^2}} \right)}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}}$
Cancel the whole square term from numerator and denominator
We get,
${h^2} + {k^2} = \dfrac{{{c^2}}}{{\left( {{a^2} + {b^2}} \right)}}$ ………(iv)
Squaring the equation (i) and substitute the value of $\dfrac{{{c^2}}}{{\left( {{a^2} + {b^2}} \right)}}$ in this equation (iv)
We get,
${h^2} + {k^2} = {P^2}$
Replace (h, k) by (X,Y) in the above equation we get
${X^2} + {Y^2} = {P^2}$

In option D it is given, so the correct answer for the locus of the point of intersection of perpendicular straight lines which are at constant distance ‘P’ from the origin is ${X^2} + {Y^2} = {P^2}$ or option D.

Note:
1.The perpendicular distance of a point $({x_1},{y_1})$from the line $ax + by + c = 0$is $P = \dfrac{{\left| {a{x_1} + b{y_1} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$
2. The foot of perpendicular $({x_1},{y_1})$to the line $ax + by + c = 0$is $\dfrac{{x - {x_1}}}{a} = \dfrac{{y - {y_1}}}{b} = - \dfrac{{\left( {a{x_1} + b{y_1} + c} \right)}}{{{a^2} + {b^2}}}$
3. The locus is a curve or other figure formed by all the points satisfying a particular equation of the relation between coordinates, or by a point, line, or surface moving according to mathematically defined conditions.