Question

The locus of the point $\left( h,k \right)$ , if the point $\left( \sqrt{3h},\sqrt{3k+2} \right)$ lies on the line $x-y-1=0$, is a ?
(A) Straight line
(B) Circle
(C) Parabola
(D) None of these

Answer 1

For answering this question we have been asked to find the locus of the point $\left( h,k \right)$ , if the point $\left( \sqrt{3h},\sqrt{3k+2} \right)$ lies on the line $x-y-1=0$ . From the basic concepts we know that for the general equation $a{{x}^{2}}+b{{y}^{2}}+2gx+2fy+2hxy+c=0$ and if ${{h}^{2}}=ab,\Delta =abc+2fgh-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}\ne 0$ then it is a parabola.

Complete step by step solution:
Now considering from the question we have been asked to find the locus of the point $\left( h,k \right)$ , if the point $\left( \sqrt{3h},\sqrt{3k+2} \right)$ lies on the line $x-y-1=0$ .
From the basic concepts we know that for the general equation $a{{x}^{2}}+b{{y}^{2}}+2gx+2fy+2hxy+c=0$ and if ${{h}^{2}}=ab,\Delta =abc+2fgh-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}\ne 0$ then it is a parabola.
Now for expressing the given condition in this form we will substitute the given point $\left( \sqrt{3h},\sqrt{3k+2} \right)$ in the given line equation $x-y-1=0$ .
By substituting we will have $\Rightarrow \sqrt{3h}-\sqrt{3k+2}-1=0$ .
By further simplifying this we will have $\Rightarrow \sqrt{3h}=\sqrt{3k+2}+1$ .
For more simplifying this expression we will performing squaring on both sides of the expression and further reducing it we will have
$\begin{aligned} & \Rightarrow {{\left( \sqrt{3h} \right)}^{2}}={{\left( \sqrt{3k+2}+1 \right)}^{2}} \\\ & \Rightarrow 3h=3k+2+1+2\sqrt{3k+2} \\\ & \Rightarrow 3h-3k-3=2\sqrt{3k+2} \\\ & \Rightarrow 3\left( h-k-1 \right)=2\sqrt{3k+2} \\\ \end{aligned}$
Now we will again perform squaring on both sides of the expression then we will have
$\begin{aligned} & \Rightarrow 9{{\left( h-k-1 \right)}^{2}}=4\left( 3k+2 \right) \\\ & \Rightarrow 9{{h}^{2}}+9{{k}^{2}}+9-18hk-18h+18k=12k+8 \\\ & \Rightarrow 9{{h}^{2}}+9{{k}^{2}}-18hk-18h+6k+1=0 \\\ \end{aligned}$
Hence the required locus will be $9{{x}^{2}}+9{{y}^{2}}-18xy-18x+6y+1=0$ .

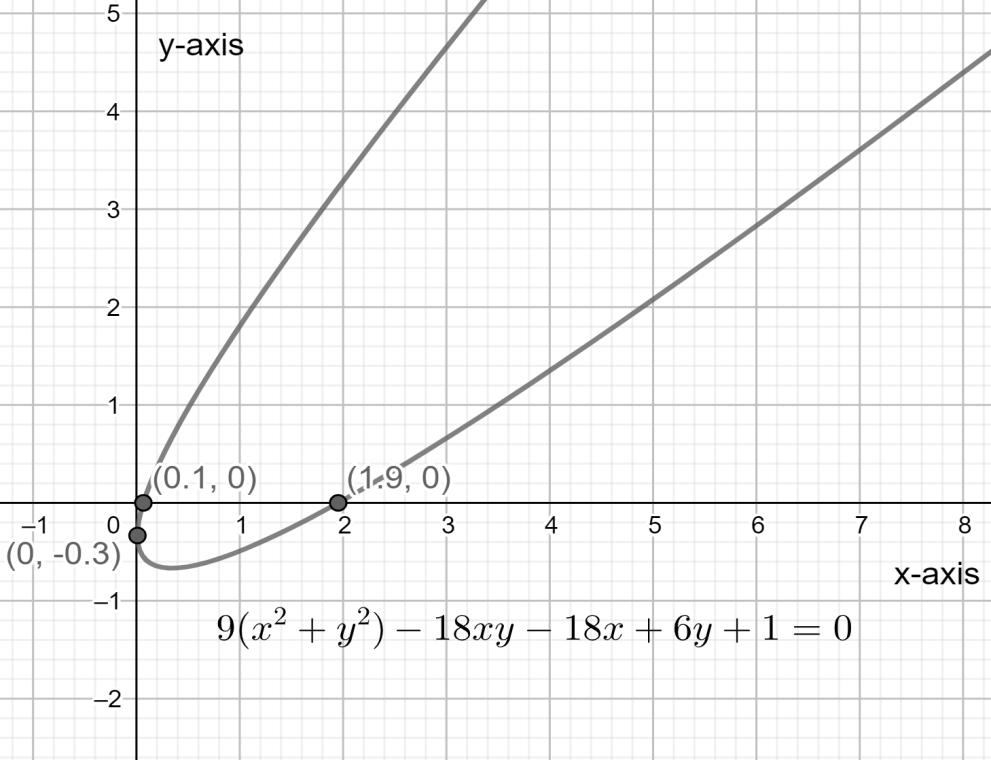
Since this locus lies in the form of $a{{x}^{2}}+b{{y}^{2}}+2gx+2fy+2hxy+c=0$and ${{h}^{2}}=ab,\Delta =abc+2fgh-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}\ne 0$ . Hence it is a parabola. Hence we will mark the option “C” as correct.

Note: During the process of answering questions of this type we should be careful with our concepts that we are going to apply and the calculations that we are going to perform. From the basic concepts we know that for the general equation $a{{x}^{2}}+b{{y}^{2}}+2gx+2fy+2hxy+c=0$ and if ${{h}^{2}}< ab,\Delta =abc+2fgh-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}\ne 0$ then it is an ellipse and if ${{h}^{2}}> ab,\Delta \ne 0$ then it is a hyperbola and if $\Delta =0,h=0,a=b$ then it is a circle.