Solveeit Logo
Login

Question

Question: The locus of the midpoints of chords of the circle \[{x^2} + {y^2} = 1\]which subtends a right angle...

The locus of the midpoints of chords of the circle x2+y2=1{x^2} + {y^2} = 1which subtends a right angle at the origin is

A.x2+y2=14{x^2} + {y^2} = \dfrac{1}{4}
B.x2+y2=12{x^2} + {y^2} = \dfrac{1}{2}
C.xy=0xy = 0
D.x2−y2=0{x^2} - {y^2} = 0

Explanation

Solution

In this question equation of the circle is given, and the coordinate of center and vertex is also given, so we will find the radius of the circle by comparing it with the length of the cord, and then the chord equation is found.

Complete step-by-step answer:
Given the center of the circle, C is at (0,0)(0,0)
R is the radius of the circle
Equation of the circle x2+y2=1{x^2} + {y^2} = 1

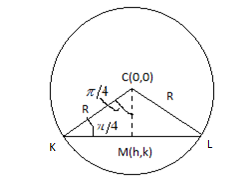
In the figure, we can see line CM is perpendicular to the KL; hence we apply the right-angled property inΔCKM\Delta CKM; therefore, the length of line CM will be
CM=Rsin⁡π4=R2−−(i)CM = R\sin \dfrac{\pi }{4} = \dfrac{R}{{\sqrt 2 }} - - (i) [Sincesin⁡π4=12\sin \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}]
By squaring both sides of the equation (i), we can further write

(CM)2=(R2)2 ⇒(CM)2=R22−−(ii)  {\left( {CM} \right)^2} = {\left( {\dfrac{R}{{\sqrt 2 }}} \right)^2} \\\ {\Rightarrow \left( {CM} \right)^2} = \dfrac{{{R^2}}}{2} - - (ii) \\\

Now apply the distance formula in the line CM whose vertices are given as (0, 0) and (h, k), respectively

(CM)2=(h−0)2+(k−0)2 ⇒(CM)2=h2+k2−−(iii)  {\left( {CM} \right)^2} = {\left( {h - 0} \right)^2} + {\left( {k - 0} \right)^2} \\\ \Rightarrow { \left( {CM} \right)^2} = {h^2} + {k^2} - - (iii) \\\

Where (CM)2=R22{\left( {CM} \right)^2} = \dfrac{{{R^2}}}{2} from equation (ii)
Hence by comparing equation (ii) and (iii), we can write
h2+k2=R22−−(iv){h^2} + {k^2} = \dfrac{{{R^2}}}{2} - - (iv)
Since the equation of the circle is given hence by replacing h, k by x, y and radius R with 1 in equation (iv), we get the equation as

x2+y2=122 ⇒x2+y2=12  {x^2} + {y^2} = \dfrac{{{1^2}}}{2} \\\ \Rightarrow {x^2} + {y^2} = \dfrac{1}{2} \\\

Hence the locus of the midpoints x2+y2=12{x^2} + {y^2} = \dfrac{1}{2}
Option (B) is correct.

Note: A chord of a circle is the straight line drawn between the ends point of the circle, where the diameter is the longest chord passing through the center, joining both endpoints at the circumference.