Question

The locus of the mid points of the perpendiculars drawn from points on the line, $x = 2y$ to the line $x = y$ is:
A. $7x - 5y = 0$
B. $5x - 7y = 0$
C. $2x - 3y = 0$
D. $3x - 2y = 0$

Answer 1

We will start by constructing the figure, for the line $x = 2y$ we will let the point on the line as $P = \left( {2a,a} \right)$ and for the line $x = y$, the point on the line will be $Q = \left( {b,b} \right)$. After this we will use the method of the slope of the line $PQ$ to find the equation in terms of $h$ and $k$. Next, we will use the mid-point formula to find another equation between the points $P$ and $Q$. Thus, using both the equations, we will get the equation of locus in terms of $h$ and $k$ and thus, we will replace it by $x$ and $y$ and get the desired result.

Complete step by step answer:

We will first construct the figure showing two lines, $x = 2y$ and $x = y$. We will also let that the point $P = \left( {2a,a} \right)$ lies on the line $x = 2y$ and the point $Q = \left( {b,b} \right)$ lies on the line $x = y$.

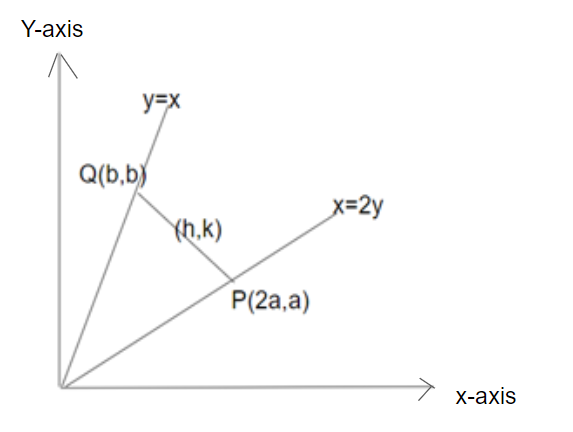
Now, as we know that the slope of the line is given by $S = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ so, we will find the equation of the slope of the line $PQ$ by substituting $\left( {{x_1},{y_1}} \right) = \left( {2a,a} \right)$ and $\left( {{x_2},{y_2}} \right) = \left( {h,k} \right)$,
Thus, we have,

$$\Rightarrow \dfrac{{k - a}}{{h - 2a}} = - 1 \\\ \Rightarrow k - a = - h + 2a \\\ \Rightarrow a = \dfrac{{h + k}}{3} \\\$$

Hence, we get the first equation as $a = \dfrac{{h + k}}{3}$----(1)
Also, we will use the mid-point formula on the points lying on the line $PQ$.
Thus, we get,
$\Rightarrow 2h = 2a + b$ and $2k = a + b$
Thus, we will use the elimination method to find another equation by eliminating $b$ from both the equations and find the value of $a$,
$\Rightarrow a = 2h - 2k$---(2)
Next, we will use equation (1) and (2) to eliminate $a$ from it.

$$\Rightarrow \dfrac{{k + h}}{3} = 2\left( {h - k} \right) \\\ \Rightarrow k + h = 6\left( {h - k} \right) \\\$$

Now, we can replace the point $\left( {h,k} \right)$ with $\left( {x,y} \right)$.
Hence, we get the equation as:

$$\Rightarrow 6x - 6y = x + y \\\ \Rightarrow 5x = 7y \\\ \Rightarrow 5x - 7y = 0 \\\$$

Thus, we can conclude that the equation of the locus is $5x - 7y = 0$.

Note: We have used the concept of slope of the equation using the formula $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ and then the midpoint formula to find the equations. To determine the equation of the locus of the lines given we need to answer in terms of point $\left( {x,y} \right)$. Constructing the figure makes the concept clearer and more understandable. While substituting the points in the formula of the slope of the line do it properly. Calculations should be done properly in each step.