Question

The locus of the centers of the circles which touch the two circle ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$and${{x}^{2}}+{{y}^{2}}=4ax$ externally is.

• A. $12{{x}^{2}}-4{{y}^{2}}-24ax+9{{a}^{2}}=0$

• B. $12{{x}^{2}}+4{{y}^{2}}-24ax+9{{a}^{2}}=0$

• C. $12{{x}^{2}}-4{{y}^{2}}+24ax+9{{a}^{2}}=0$

• D. $12{{x}^{2}}+4{{y}^{2}}+24ax+9{{a}^{2}}=0$

Answer 1

Hint: Take the equations and write their centers and radius. Then consider the center of a circle in which you want to find the locus of the center. Then equate it and solve it. You will get the answer.

Complete step-by-step answer:
A locus is the set of all points (usually forming a curve or surface) satisfying some condition. For example, the locus of points in the plane equidistant from a given point is a circle, and the set of points in three-space equidistant from a given point is a sphere.

A locus of points usually results in a curve or surface. For instance, in our hiking example, the locus of points 5 miles from our starting point resulted in a curve that's a circle.

Now, how do we usually represent curves algebraically? If you're thinking we use an equation, you're exactly right.
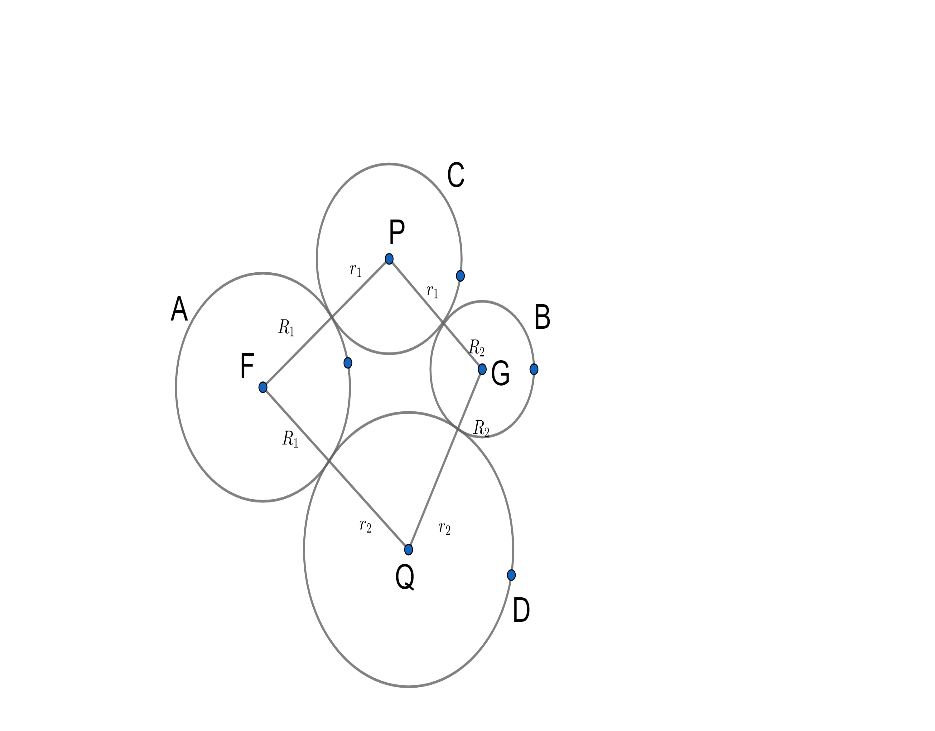
Let $A$ and $B$ are the given two circles with radii ${{R}_{1}}$ and ${{R}_{2}}$​ respectively and their centers are $F$ and $G$respectively.
Let $C$ and $D$ are variable circles so that each circle meets the given circles $A$ and $B$ externally.

Let ${{r}_{1}}$​ be the radius of the circle $C$ and $P$ be its center. Let ${{r}_{2}}$​ be the radius of the circle $D$ and $Q$ be its center.
$PF={{R}_{1}}+{{r}_{1}},PG={{R}_{2}}+{{r}_{1}}$
Now subtracting above both we get,
$PF-PG={{R}_{1}}-{{R}_{2}}$
Also $QF={{R}_{1}}+{{r}_{2}},QG={{R}_{2}}+{{r}_{2}}$
Again subtracting we get,
$QF-QG={{R}_{1}}-{{R}_{2}}$

Hence locus of centers of touching circles is a set of points so that the difference between the distances from two given fixed points ( here $F$and $G$ ) to the point in locus is constant.
This locus is hyperbola and the fixed points$F$and $G$ (Centers of given circles ) are foci of hyperbola.

Now we have given ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$,
So let the center be${{C}_{1}}$,
${{C}_{1}}(0,0)$because we can see the coefficient of$x$and$y$is zero.
And radius ${{r}_{1}}=\sqrt{a}$.

Now again one equation is given that${{x}^{2}}+{{y}^{2}}=4ax$,
So let the center be${{C}_{2}}$,
${{C}_{2}}(2a,0)$because we can see a coefficient of$y$is zero.
And radius ${{r}_{2}}=\sqrt{{{g}^{2}}+{{f}^{2}}+{{c}^{2}}}=\sqrt{0+0+{{(2a)}^{2}}}=2a$.

Let the radius of the circle of which we want to find a locus be$r$.
And the center is$C(h,k)$.
So now using distance formula we get,
$\begin{aligned} & r+a=\sqrt{{{h}^{2}}+{{(k-a)}^{2}}} \\\ & r+2a=\sqrt{{{h}^{2}}+{{(k-2a)}^{2}}} \\\ \end{aligned}$

Let${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ be the variable circle.
Since it touches the given circle easily,
$\sqrt{{{(-g-0)}^{2}}+{{(-f-0)}^{2}}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}+a$ ...(1)
and, $\sqrt{{{(-g-2a)}^{2}}+{{(-f-0)}^{2}}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}+2a$ ...(2)
Subtracting (1) from (2), we get
$\sqrt{{{(g+2a)}^{2}}+{{f}^{2}}}=\sqrt{{{g}^{2}}+{{f}^{2}}}+a$
Squaring both sides, we get
${{(g+2a)}^{2}}+{{f}^{2}}={{(\sqrt{{{g}^{2}}+{{f}^{2}}}+a)}^{2}}$

$\begin{aligned} & {{g}^{2}}+4ga+4{{a}^{2}}+{{f}^{2}}={{g}^{2}}+{{f}^{2}}+2a\sqrt{{{g}^{2}}+{{f}^{2}}}+{{a}^{2}} \\\ & 4ag+3{{a}^{2}}=2a\sqrt{{{g}^{2}}+{{f}^{2}}} \\\ \end{aligned}$
Now divide the whole equation by $a$we get,
$4g+3a=2\sqrt{{{g}^{2}}+{{f}^{2}}}$
Now square both sides we get,
${{\left( 4g+3a \right)}^{2}}={{\left( 2\sqrt{{{g}^{2}}+{{f}^{2}}} \right)}^{2}}$
${{\left( (-4)(-g)+3a \right)}^{2}}=4\left( {{g}^{2}}+{{f}^{2}} \right)$
So the locus of the centre$(-g,-f)$is${{(-4x+3a)}^{2}}=4({{x}^{2}}+{{y}^{2}})$,
So simplifying above we get,

$\begin{aligned} & 16{{x}^{2}}+9{{a}^{2}}-24ax=4{{x}^{2}}+4{{y}^{2}} \\\ & 12{{x}^{2}}-4{{y}^{2}}-24ax+9{{a}^{2}}=0 \\\ \end{aligned}$
So we get locus of the centre as$12{{x}^{2}}-4{{y}^{2}}-24ax+9{{a}^{2}}=0$.
So the correct answer is an option(A).

Note: Read the question carefully. You should know the concept of locus of point and locus of the center. Don’t jumble yourself in transferring the equations. Most of the students make mistakes in minus signs, So avoid the mistake.