Question

The locus of point X which moves inside the rhombus PQRS such that its distance from S is equal to its distance from Q is the line

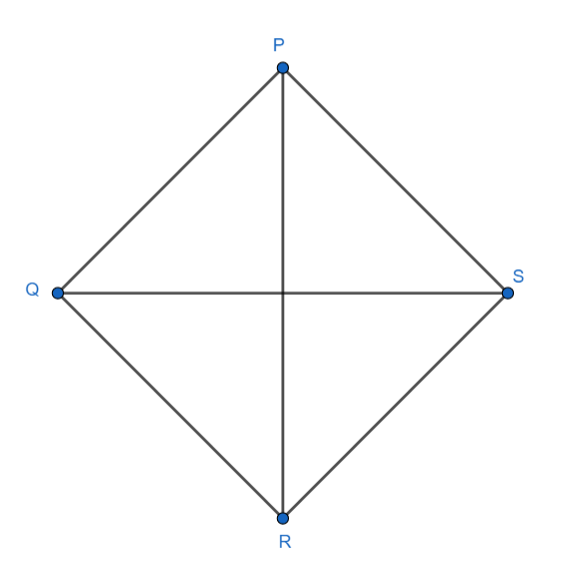
[a] PQ
[b] QR
[c] PR
[d] RS

Answer 1

Hint: Check option-wise and verify which of the options is correct. In the first option take point Q on the line PQ and check if it satisfies the given condition of the locus. In the second option take point Q on the line QR and check if it satisfies the given condition of the locus. In option, D take point S on RS and check if it satisfies the given condition of the locus. Prove for any point M on PR the given condition of the locus is satisfied.
Complete step-by-step answer:

We will check option-wise and check which of the options are correct.
Option [a]: PQ
Point Q lies on the line PQ
Now, we have the distance of Q from Q = 0
The distance of Q from S = QS $\ne 0$
Hence the distance of Q from Q is not equal to the distance of Q from S.
Point Q does not satisfy the condition of locus
PQ is not the required locus
Option [b]: QR
Point Q lies on the line QR
Now, we have the distance of Q from Q = 0
The distance of Q from S = QS $\ne 0$
Hence the distance of Q from Q is not equal to the distance of Q from S.
Point Q does not satisfy the condition of locus
QR is not the required locus
Option [d]: RS
Point S lies on the line SR
Now, we have the distance of S from S = 0
The distance of S from Q = QS $\ne 0$
Hence the distance of S from Q is not equal to the distance of S from S.
Point S does not satisfy the condition of locus
SR is not the required locus
Option [d]: PR
Consider any point M on PR as shown

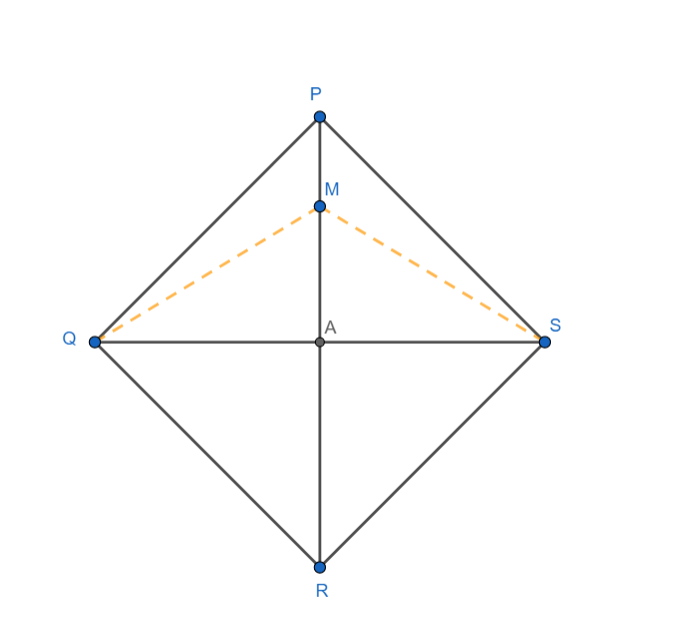
We know that the diagonals of a rhombus bisect each other at right angles.
Hence, we have AQ = AS and $\angle MAQ=\angle MAS=90{}^\circ$
Now in triangles MAQ and MAS, we have
MA = MA (common side)
QA = SA (Proved Above)
$\angle MAQ=\angle MAS$(Proved Above)
Hence, we have $\Delta MAQ\cong \Delta MAS$(By SAS congruence criterion)
Hence, we have MQ = MS(corresponding parts of congruent triangles).
Hence the distance of point M from Q is equal to its distance from S.
Hence PR is the required locus.
Note: The locus of a point equidistant from two points in a plane is the perpendicular bisector of the line segment joining the points. Hence the required locus will be the perpendicular bisector of QS. Since PR bisects QS at right angles, we have PR is a perpendicular bisector of QS and hence is the required locus.