Question
Question: The locus of point of intersection of tangents to the parabolas \[{{y}^{2}}=4\left( x+1 \right)\]...
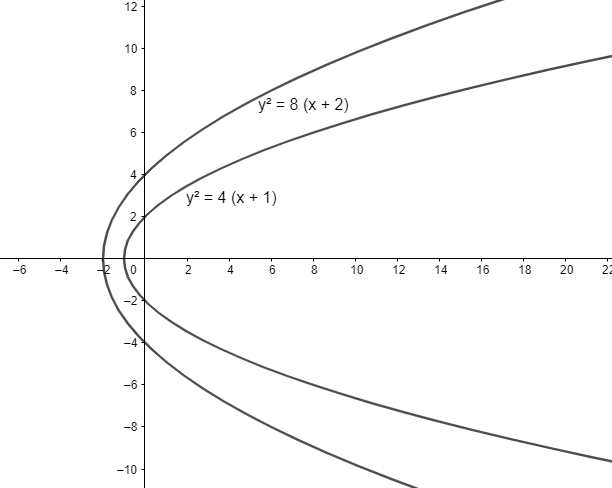
The locus of point of intersection of tangents to the parabolas y2=4(x+1)and y2=8(x+2) which are perpendicular to each other, is
(a) x+7=0
(b) x−y=4
(c) x+3=0
(d) y−x=12
Solution
Hint: To find the locus of point of intersection of tangents to the two parabolas
which are perpendicular to each other, write the equation of tangents in slope form and
solve them to find the locus of their point of intersection. Also, the product of slope of two
perpendicular lines is -1.
We have two parabolas y2=4(x+1)andy2=8(x+2).
To find the locus of points of intersection of perpendicular tangents to the two parabolas, we
will first write the equation of tangents to the parabolas in slope form.
We know that equation of tangent of a parabola of the form y2=4a(x−b)with slopem is y=m(x−b)+ma.
Let’s assume that the slope of tangents to one of the parabolas is m.
We know that the product of slopes of two perpendicular lines is -1.
So, the slope of the other tangent is m−1.
For the parabola y2=4(x+1), we have a=1,b=−1.
Substituting the above values in equation of tangent, we get y=m(x+1)+m1=mx+m1+m. (1)
For the parabola y2=8(x+2), we have a=2,b=−2.
Substituting the above values in equation of tangent, we get y=m−1(x+2)+m−12=m−x−m2−2m. (2)
Subtracting equation (1) from equation (2), we get
mx+mx+3m+m3=0.
⇒x(m+m1)+3(m+m1)=0
⇒x+3=0
We observe that the locus of points of intersection of perpendicular tangents is a straight
line. We can also find the point at which the tangent intersects the parabola. We just have to
substitute the equation of parabola in the equation of tangent and solve the equation to get
their point of intersection.
Hence, the correct answer is x+3=0 which is option (c).
Note: We can also write the equation of tangents in the point form taking the locus as point
of intersection of two tangents and then substituting the product of slopes of two tangents
as -1.
