Question

The locus of a point equidistant from two given points a and b is given by

• A. $\lbrack\mathbf{r} - \frac{1}{2}(\mathbf{a} + \mathbf{b})\rbrack.(\mathbf{a} - \mathbf{b}) = 0$
• B. $\lbrack\mathbf{r} - \frac{1}{2}(\mathbf{a} - \mathbf{b})\rbrack.(\mathbf{a} + \mathbf{b}) = 0$
• C. $\lbrack\mathbf{r} - \frac{1}{2}(\mathbf{a} + \mathbf{b})\rbrack.(\mathbf{a} + \mathbf{b}) = 0$
• D. $\lbrack\mathbf{r} - \frac{1}{2}(\mathbf{a} - \mathbf{b})\rbrack.(\mathbf{a} - \mathbf{b}) = 0$

Answer 1

Answer: (A)

$\lbrack\mathbf{r} - \frac{1}{2}(\mathbf{a} + \mathbf{b})\rbrack.(\mathbf{a} - \mathbf{b}) = 0$

Answer 2

Let $P(\mathbf{r})$ be equidistant from $A(\mathbf{a})$ and $B(\mathbf{b})$ and $PM$ be perpendicular to $AB.$

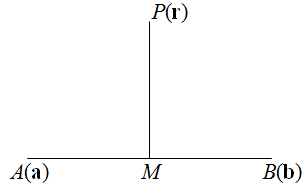
Then $M$ is the mid point of $AB.$

Position vector of $M$ is $\frac{1}{2}(\mathbf{a} + \mathbf{b}).$

$\overset{\rightarrow}{PM}.\overset{\rightarrow}{BA} = 0$ or $\left\lbrack \mathbf{r} - \frac{1}{2}(\mathbf{a} + \mathbf{b}) \right\rbrack.(\mathbf{a} - \mathbf{b}) = 0.$