Question

The locus of a point equidistant from two given points whose position vectors are a and b is equal to

• A. $\left[ \mathbf { r } - \frac { 1 } { 2 } ( \mathbf { a } + \mathbf { b } ) \right] \cdot ( \mathbf { a } + \mathbf { b } ) = 0$
• B. $\left[ \mathbf { r } - \frac { 1 } { 2 } ( \mathbf { a } + \mathbf { b } ) \right] \cdot ( \mathbf { a } - \mathbf { b } ) = 0$
• C.
• D.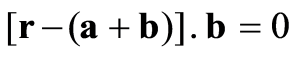

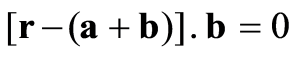
Answer 1

Answer: (B)

$\left[ \mathbf { r } - \frac { 1 } { 2 } ( \mathbf { a } + \mathbf { b } ) \right] \cdot ( \mathbf { a } - \mathbf { b } ) = 0$

Answer 2

Let $P ( \mathbf { r } )$ be a point on the locus.

$\therefore$ $A P = B P$

̃ $| \mathbf { r } - \mathbf { a } | = | \mathbf { r } - \mathbf { b } |$ ̃ $| \mathbf { r } - \mathbf { a } | ^ { 2 } = | \mathbf { r } - \mathbf { b } | ^ { 2 }$

̃ $( \mathbf { r } - \mathbf { a } ) \cdot ( \mathbf { r } - \mathbf { a } ) = ( \mathbf { r } - \mathbf { b } ) \cdot ( \mathbf { r } - \mathbf { b } )$

̃ ̃

$\therefore$ . This is the locus of P.