Question
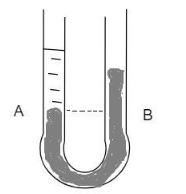
Question: The liquids shown in fig. in the two arms are mercury (specific gravity\( = 13.6\) ) and water. If t...
The liquids shown in fig. in the two arms are mercury (specific gravity=13.6 ) and water. If the difference of heights of the mercury columns is 2cm , find the height h of the water column.
(A) 27cm
(B) 30cm
(C) 35cm
(D) 44cm
Solution
The points A and B are at the same level, hence the pressure of the liquids at the same medium is equal. Substitute the formula of the pressure in this relation and substitute the known values to find the answer for the height of the water in the tube.
Formula used:
The formula of the pressure is given by
P=fgh
Where P is the pressure of the liquid, f is the specific gravity of the liquid, g is the acceleration due to gravity and the h is the height of the liquid present in the manometer.
Complete step by step solution:
It is given that the
Specific gravity of the mercury =13.6
Height of the mercury is 2cm
In general, the pressure at the same level in the same medium is the same.
Hence the pressure at a point A must be equal to the pressure at the point B .
Pressure at A = Pressure at B
Substituting the formula of the pressure in the above step.
fwgh=fmgH
Substituting the values of the specific gravity and the height of the mercury.
h=13.6×2
By performing the basic arithmetic operation in the above step, we get
h=27.2≈27cm
Hence the height of the water column in the manometer is 27cm .
Thus the option (A) is correct.
Note: In this question, the specific gravity of the water is substituted as one. In the manometer, when the positive pressure is given to one arm, then the liquid in the other arm moves up. This change or difference in height gives the pressure.
