Question

The lines $x + 2ay + a = 0$, $x + 3by + b = 0$, $x + 4cy + c = 0$ are concurrent then a, b, c are in

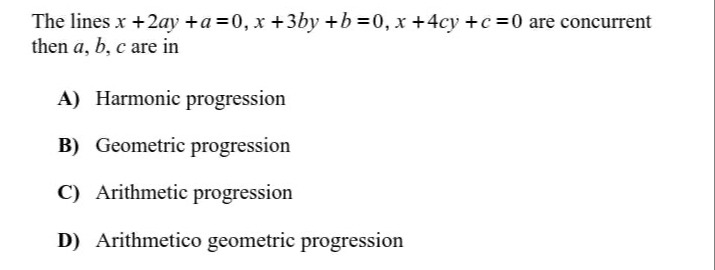
• A. Harmonic progression
• B. Geometric progression
• C. Arithmetic progression
• D. Arithmetico geometric progression

Answer 1

Answer: (A)

Harmonic progression

Answer 2

The condition for three lines $A_1x + B_1y + C_1 = 0$, $A_2x + B_2y + C_2 = 0$, and $A_3x + B_3y + C_3 = 0$ to be concurrent is that the determinant of their coefficients is zero: $\begin{vmatrix} A_1 & B_1 & C_1 \\ A_2 & B_2 & C_2 \\ A_3 & B_3 & C_3 \end{vmatrix} = 0$ The given lines are:

1. $x + 2ay + a = 0$
2. $x + 3by + b = 0$
3. $x + 4cy + c = 0$

Substituting the coefficients into the determinant: $\begin{vmatrix} 1 & 2a & a \\ 1 & 3b & b \\ 1 & 4c & c \end{vmatrix} = 0$ To simplify, we can apply column operations. Let's perform $C_2 \to C_2 - 2C_3$: $\begin{vmatrix} 1 & 2a - 2a & a \\ 1 & 3b - 2b & b \\ 1 & 4c - 2c & c \end{vmatrix} = 0$ $\begin{vmatrix} 1 & 0 & a \\ 1 & b & b \\ 1 & 2c & c \end{vmatrix} = 0$ Now, expand the determinant along the second column: $-0 \cdot \begin{vmatrix} 1 & b \\ 1 & c \end{vmatrix} + b \cdot \begin{vmatrix} 1 & a \\ 1 & c \end{vmatrix} - 2c \cdot \begin{vmatrix} 1 & a \\ 1 & b \end{vmatrix} = 0$ $b(1 \cdot c - a \cdot 1) - 2c(1 \cdot b - a \cdot 1) = 0$ $b(c - a) - 2c(b - a) = 0$ $bc - ab - 2bc + 2ac = 0$ $-bc - ab + 2ac = 0$ Rearranging the terms, we get: $2ac = ab + bc$ Assuming $a, b, c$ are non-zero (for the progressions to be well-defined), we can divide the entire equation by $abc$: $\frac{2ac}{abc} = \frac{ab}{abc} + \frac{bc}{abc}$ $\frac{2}{b} = \frac{1}{c} + \frac{1}{a}$ This equation can be rewritten as: $\frac{1}{a} + \frac{1}{c} = \frac{2}{b}$ This is the condition for $\frac{1}{a}, \frac{1}{b}, \frac{1}{c}$ to be in Arithmetic Progression (AP). If the reciprocals of a set of numbers are in AP, then the numbers themselves are in Harmonic Progression (HP).