Question

The lines ${L_1}:y - x = 0$ and ${L_2}:2x + y = 0$ intersect the line ${L_3}:y + 2 = 0$at P and Q respectively. The bisector of the acute angle between ${L_1}$ and ${L_2}$ intersects ${L_3}$ at R.
Statement I : the ratio of $PR:RQ$ equals $2\sqrt 2 :5$
Statement II: In any triangle, the angle bisector divides the triangle into two similar triangles.
(A) Both Statement-1 and Statement-2 is true, also Statement-2 is a correct explanation for Statement-1.
(B) Both Statement-1 and Statement-2 is true, but Statement-2 is not a correct explanation for Statement-1.
(C) As Statement-1 is true, and Statement-2 is false
(D) As Statement-2 is true, and Statement-1 is false

Answer 1

For solving this question we will first find the point of intersection of lines and then find the value of sides of the triangle by distance formula and check the statements whether they are true or false.

Complete step-by-step answer:

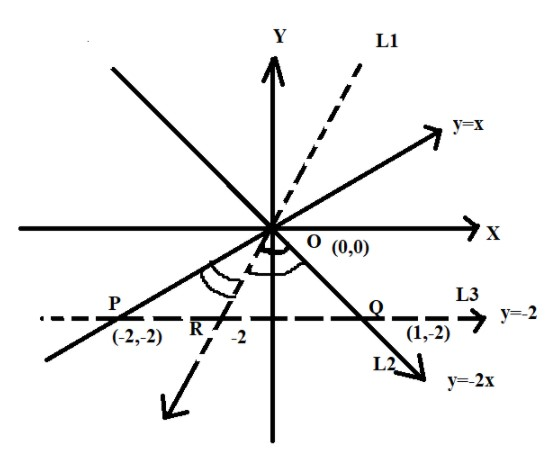
First we draw a figure according to the question which consists of three lines and point of intersection of these lines.
As given in the question
Equation of line ${L_1}$ is $y - x = 0 \\\ y = x - - - - - - - (1) \\\$
Equation of line ${L_2}$ is $2x + y = 0 \\\ y = - 2x - - - - - (2) \\\$
Equation of line ${L_3}$ is $y + 2 = 0 \\\ y = - 2 - - - - - - - - (3) \\\$
Now the line ${L_1}$ and line ${L_3}$ intersects at point P.
Now putting the value of equation (3) in equation (1) we get the coordinates of P is $( - 2, - 2)$
Also line ${L_2}$ and ${L_3}$ intersect at point Q.
Now putting the value of equation (3) in equation (2) we get the coordinates of point Q is $(1, - 2)$
Now the lines ${L_1}$ and ${L_2}$ intersect at point O. the coordinates of O is $(0,0)$ because they both intersect at origin.
Now we find the value of OP by distance formula which is
$d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
Where d is the distance between two points, $({x_1},{y_1})$ are the coordinates of first point, $({x_2},{y_2})$ are the coordinates of the second point.
Now putting the value of the points O $(0,0)$ and P$( - 2, - 2)$ we get
$OP = \sqrt {{{( - 2 - 0)}^2} + {{( - 2 - 0)}^2}} \\\ = \sqrt {{{( - 2)}^2} + {{( - 2)}^2}} \\\ = \sqrt {4 + 4} \\\ = \sqrt 8 \\\ = 2\sqrt 2 \\\$
$\therefore$ So the value of $OP = 2\sqrt 2$
Now we find the value of OQ by distance formula which is
$d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$
Where d is the distance between two points, $({x_1},{y_1})$ are the coordinates of first point, $({x_2},{y_2})$ are the coordinates of the second point.
Now putting the value of the points O$(0,0)$and Q$(1, - 2)$ we get
$OQ = \sqrt {{{(1 - 0)}^2} + {{( - 2 - 0)}^2}} \\\ = \sqrt {{{(1)}^2} + {{( - 2)}^2}} \\\ = \sqrt {1 + 4} \\\ = \sqrt 5 \\\$
$\therefore$So the value of $OQ = \sqrt 5$
Now, in $\Delta OPQ$, the angle bisector OR of $\angle O$ divides PQ in the ratio as
$\Rightarrow OP:OQ = PR:RQ$
Which gives us
$\Rightarrow 2\sqrt 2 :\sqrt 5 = PR:RQ$
Hence Statement I is correct.
Now the angle bisector OR does not divide $\Delta OPQ$ into two similar triangles the other two angles except the angle which is bisected is not equal to each other.
Hence Statement II is false.

So, the correct answer is “Option C”.

Note: For solving these type of problems we determine the value of the coordinates of the point of intersection of the line with the help of distance formula. For finding the ratio of the sides of the triangle we find the value of the sides of the triangle and compare the ratios of the sides of the triangle and the arms of the angle $\angle POR,\angle QOR$ as OR is the angle bisector. This proves the statement I and II are correct or not.