Question

The linear mass density $(\lambda )$ of a rod of length $L$ kept along $x-axis$, varies as $\lambda =\alpha +\beta x$, where $\alpha$ and $\beta$are positive constants.The centre of mass of the rod is at?

Answer 1

In order to answer the above question, first we will understand what we mean by centre of mass of a system of particles. We will also derive the equation to calculate the centre of mass. Using the formula for the centre of mass, we will find the centre of mass of the rod asked in the question.

Formula used:
Centre of mass of a system of particles:
$CM=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+...+{{m}_{n}}{{x}_{n}}}{{{m}_{1}}+{{m}_{2}}+...+{{m}_{n}}}$
Where ${{m}_{1}},{{m}_{2}},...,{{m}_{n}}$ are the masses of every particle of the system and ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ are the position of the particles from the principal axis.

Complete step by step answer:
A point at which the entire mass of a body or all the masses of a system of particles appeared to be concentrated is known as the centre of mass of a body or system of particles.We don't need to worry about the dynamics of individual particles of the system when analysing the dynamics of the motion of the system as a whole. However, just concentrate on the dynamics of a single point that corresponds to that structure.

This particular point's motion is similar to that of a single particle whose mass is equal to the sum of all individual particles in the system and the resultant of all forces exerted on all particles in the system by surrounding bodies (or) the action of a field of force is exerted directly on that particle. The centre of mass of the system of particles is this location. When two or more objects collide or an object bursts into fragments, the idea of centre of mass (COM) is useful in studying the complicated motion of the system of objects.

Now, from the information provided in the question, we have a rod of length $L$having a linear mass density of $(\lambda )$. This linear density changes as a function of position $\lambda =\alpha +\beta x$

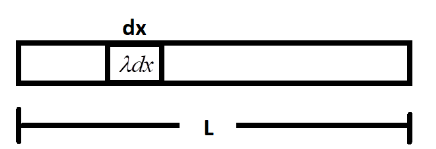
The centre of mass of the system can be given by:
$CM=\dfrac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+...+{{m}_{n}}{{x}_{n}}}{{{m}_{1}}+{{m}_{2}}+...+{{m}_{n}}}$
Where ${{m}_{1}},{{m}_{2}},...,{{m}_{n}}$are the masses of every particle of the system and ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ are the position of the particles from the principal axis.
$\Rightarrow CM=\dfrac{\sum{mx}}{\sum{m}}$
Here, the element of mass is given in terms of its density and is given by $dm=\lambda dx$. The density is distributed continuously throughout the whole rod and hence we need to take the integration in place of summation. Therefore the above equation can be written as:
$CM=\dfrac{\int\limits_{0}^{L}{(\lambda x)dx}}{\int\limits_{0}^{L}{\lambda dx}}$
Now, it is said that the density is non-uniformly distributed and varies as a function of position $\lambda =\alpha +\beta x$. Placing the value, we get
\Rightarrow CM=\dfrac{\int\limits_{0}^{L}{\left\\{ (\alpha +\beta x)(x) \right\\}dx}}{\int\limits_{0}^{L}{(\alpha +\beta x)dx}}
\Rightarrow CM=\dfrac{\int\limits_{0}^{L}{\left\\{ \alpha x+\beta {{x}^{2}} \right\\}dx}}{\int\limits_{0}^{L}{(\alpha +\beta x)dx}} \\\ \Rightarrow CM=\dfrac{\int\limits_{0}^{L}{\alpha xdx+\int\limits_{0}^{L}{\beta {{x}^{2}}dx}}}{\int\limits_{0}^{L}{\alpha dx+\int\limits_{0}^{L}{\beta xdx}}} \\\ \Rightarrow CM=\dfrac{\alpha \left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{L}+\beta \left[ \dfrac{{{x}^{3}}}{3} \right]_{0}^{L}}{\alpha \left[ x \right]_{0}^{L}+\beta \left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{L}} \\\
$\Rightarrow CM=\dfrac{\dfrac{\alpha {{L}^{2}}}{2}+\dfrac{\beta {{L}^{3}}}{3}}{\alpha L+\dfrac{\beta {{L}^{2}}}{2}}$
$\Rightarrow CM=\dfrac{{{L}^{2}}\left( \dfrac{3\alpha +2\beta L}{6} \right)}{L\left( \dfrac{2\alpha +\beta L}{2} \right)}$
$\therefore CM=\dfrac{L}{3}\left( \dfrac{3\alpha +2\beta L}{2\alpha +\beta L} \right)$

Therefore, the centre of mass of the given rod is $CM=\dfrac{L}{3}\left( \dfrac{3\alpha +2\beta L}{2\alpha +\beta L} \right)$.

Note: It is very important to note that the linear density in this case is a continuous distribution across the whole length of the rod and because of this, it becomes mandatory to use integration in place of summation in the calculation of centre of mass of the system. We also have to note here that the linear density is given as a function of position, which indicates that the linear mass density for the rod is non-uniformly distributed throughout the length of the rod.