Question

The linear density of the rod of length 1.0 m varies as$\lambda =2kg/m+(\dfrac{2kg}{{{m}^{2}}})x$, where x is the distance from its one end. The distance of its centre of mass from its end is
A. $\dfrac{2}{3}m$
B. $\dfrac{5}{9}m$
C. $\dfrac{4}{3}m$
D. $\dfrac{1}{2}m$

Answer 1

In the question, the linear density of the rod is given to us. The linear density of the rod, otherwise known as the mass density of the rod is the mass per unit area of the rod. In this question the linear density of the rod is a variable function, so we will have to integrate the function by taking a small element in order to get the total mass of the rod.

Complete step-by-step solution
Before we start solving the question that is given to us, let us take a look at all the parameters that are given to us in the above question
Length of the rod = l = 1.0 m
Linear Density = $\lambda =2kg/m+(\dfrac{2kg}{{{m}^{2}}})x$
Where x is the distance from one of its end
Now,
Let us consider a very small element of the rod of length dx at a distance x from one of the ends.

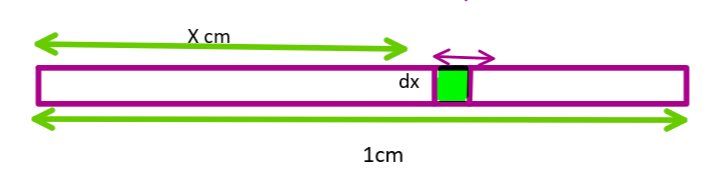
So,
The mass of the element dx will be,
$\Rightarrow dm=\lambda dx$
$\Rightarrow dm=(2+2x)dx$
Now,
Integrating on the both side
$\Rightarrow M=\int\limits_{0}^{1}{dm}=\int\limits_{0}^{1}{(2+2x)dx}$
Where, M is the weight of the whole rod
$\Rightarrow M=[(2x+\dfrac{2{{x}^{2}}}{2})]_{0}^{1}$
$\Rightarrow M=3kg$
Now, for the centre of mass
$\Rightarrow {{x}_{cm}}=\dfrac{\int{xdm}}{\int{dm}}$
$\Rightarrow {{x}_{cm}}=\dfrac{\int\limits_{0}^{1}{xdm}}{\int\limits_{o}^{q}{dm}}$
$\Rightarrow {{x}_{cm}}=\dfrac{\int\limits_{0}^{1}{x(2+2x)dx}}{\int\limits_{o}^{q}{(2+2x)dx}}$
$\Rightarrow {{x}_{cm}}=[\dfrac{(\dfrac{2{{x}^{2}}}{2}+\dfrac{2{{x}^{3}}}{3})}{2x+\dfrac{2{{x}^{2}}}{2}}]_{0}^{1}$
$\Rightarrow {{x}_{cm}}=\dfrac{1+\dfrac{2}{3}}{3}$
$\Rightarrow {{x}_{cm}}=\dfrac{5}{9}m$
So, the centre of mass of the rod will be at $\dfrac{5}{9}m$ from one of its end
So, the correct answer to this question will be Option – C, i.e., $\dfrac{5}{9}m$

Note: Keep in mind that there could be two answers to this question, depending on which end we are taking. The two answers will be $\dfrac{5}{9}m$ or $\dfrac{4}{9}m$. In this question, the center of mass is $\dfrac{5}{9}m$ away from the end with the smaller mass density.