Question

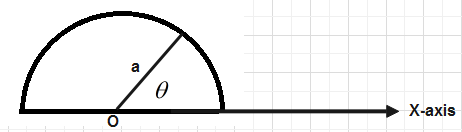
The linear charge density on the rim of the semi-circular wire is given by $\beta \theta$, where $\beta$ is a constant and $\theta$ is the angle measured from X-axis as shown in the figure .Find the total charge .The radius of semicircle is a. The total charge

a) $a\beta \dfrac{\pi }{2}$
b)$a\beta \dfrac{{{\pi }^{2}}}{2}$
c)$a\beta \pi$
d)$a\beta \dfrac{\pi }{4}$

Answer 1

In such types of questions where charge distribution is continuous firstly we have to calculate for a small charge element then we have to integrate it to get the complete value of charge over that surface. Here charge is linearly distributed so we have to use the linear charge density concept for solving this question.

Complete step-by-step solution:
Linear charge distribution is defined as charge distributed uniformly over its entire length and its magnitude is calculated by the relation as linear charge density which is equal to charge per unit length.
Surface charge distribution is defined as charge distributed over its entire area.
Volume charge distribution is defined as charge distributed over its entire volume. These all distributions come under continuous charge distribution and they do not follow the principle of superposition.
Here in the question, linear charge density on the rim of semi-circular wire is given as$\beta \theta$.
Let us assume the linear charge density is represented by symbol $\lambda$
so, linear charge density can be written as
$\lambda =\beta \theta$- - - - - - - - - (Equation 1).
Since linear charge density is defined as charge per unit length.
\therefore $$$$Linear\\_ch\arg e\\_density=\dfrac{Ch\arg e}{Length}
$\Rightarrow ch\arg e=\lambda \times Length$
We will take a small charge dq for a small angle$d\theta$.
So, $dq=\lambda ad\theta$- - - - - - - - - (Equation 2)
Now for calculating the total charge we will integrate this small charge from $0\\_to\\_\pi$because charge is distributed over a semicircular ring and the complete angle of a semi circular ring is $\pi$.
So, total charge can we written as
$q=\int\limits_{0}^{\pi }{dq}$
Put the value of dq from Equation 2,we get
$q=\int\limits_{0}^{\pi }{\lambda ad\theta }$
Put the value of linear charge density from equation 1,we get
$q=\int\limits_{0}^{\pi }{\beta \theta ad\theta }$
$q=\beta a\int\limits_{0}^{\pi }{\theta d\theta }$- - - - - - - - - (Equation 3)
Now we integrate this above equation , we get
$q=\beta a{{\left[ \dfrac{{{\theta }^{2}}}{2} \right]}^{\pi }}_{0}$

& \Rightarrow q=\beta a\left[ \dfrac{{{\pi }^{2}}}{2}-0 \right] \\\ & \therefore q=\beta a\dfrac{{{\pi }^{2}}}{2} \\\ \end{aligned}$$ This is the required expression for total charge on the rim of a semi circular ring. **So, Correct Option is B.** **Note:** Charge distribution is of two types: - Discrete charge distribution and continuous charge distribution. In discrete charge distribution charge is distributed in such a way that it can be identified individually and its calculation is done by the principle of superposition which is based on the logic of vector sum.