Question

The linear charge density on a dielectric ring of radius R varies with θ as $\lambda = {\lambda _0}\cos \dfrac{\theta }{2}$, where ${\lambda _0}$
is constant. Find the potential at the center O of the ring [in volt].

Answer 1

Hint: Charge is non uniformly distributed over the circular structure. Both in the top portion positive charge is distributed and in the bottom half the positive charge is distributed. We use potential formula to find out potential due to small strip at the center of the ring and we will integrate it over the entire ring

Formula used:
$V = \dfrac{{kq}}{r}$

Complete answer:
By using the electric potential due to a small charged element formula, we will find out the potential at the center of the ring and we will integrate it over the whole ring. Here charge distribution density is dependent on angle and it is not constant. So we will integrate that too. Consider the ring below.

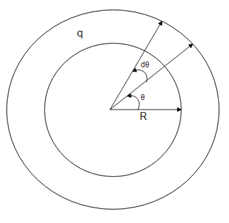
Charge is not uniformly distributed over the length of the ring. It is varying with angle theta. That angle we can take either with horizontal or with vertical because the ring is a symmetrical structure.
Linear charge density is varying with angle theta. So we have
\eqalign{ & \lambda = \dfrac{q}{l} = \dfrac{{dq}}{{dl}} \cr & \therefore dq = \lambda \left( {dl} \right) \cr}
Potential is given as
\eqalign{ & V = \dfrac{{kq}}{r} \cr & \Rightarrow dV = \dfrac{{k\left( {dq} \right)}}{r} \cr & \Rightarrow dV = \dfrac{{k\left( {\lambda \left( {dl} \right)} \right)}}{r} \cr & \Rightarrow \int\limits_0^V {dV} = \int\limits_0^{2\pi } {\dfrac{{k\left( {{\lambda _0}\cos \dfrac{\theta }{2}\left( {rd\theta } \right)} \right)}}{r}} \cr & \Rightarrow V - 0 = 2k{\lambda _0}\left[ {\sin \dfrac{\theta }{2}} \right]_0^{2\pi } = 0 \cr & \therefore V = 0 \cr}
Hence potential at the center of the ring will be zero.
If the charge distribution is not dependent on the angle and if it is constant, then we will certainly get different values for the potential.

Note:
If the charge distributed is of uniform then the y components will get cancelled and x components will get add up. For a complete ring of the same charge distribution, the field at center will be zero. In order to find out the electric field at the center for the non uniform charge distribution, integration is needed just like above but with electric field formula this time.