Question

The line $y = \sqrt 3$ meets the graph $y = \tan x$, where $x \in \left( {0,\dfrac{\pi }{2}} \right)$, in $k$points. What is $k$ equal to?
A.One
B.Two
C.Three
D.Infinity

Answer 1

Hint: The solution set for the two graphs , say $y = f\left( x \right)$ and $y = g\left( x \right)$ comprises of the solution of the equation $f\left( x \right) = g\left( x \right)$. Therefore, for the given equation, equate $\sqrt 3$ to the $\tan x$ to form the solution set. Use the condition given,$x \in \left( {0,\dfrac{\pi }{2}} \right)$ to find the value of $k$.

Complete step-by-step answer:
The solution set for the intersection of the two graphs, say $y = f\left( x \right)$ and $y = g\left( x \right)$ will contain the solution of the equation $f\left( x \right) = g\left( x \right)$.
We are given two equations $y = \sqrt 3$ and $y = \tan x$. The intersection of these two graphs will be the solution set for the equation $\sqrt 3 = \tan x$.
Taking ${\tan ^{ - 1}}$ on both sides, we get
${\tan ^{ - 1}}\left( {\sqrt 3 } \right) = {\tan ^{ - 1}}\left( {\tan x} \right)$
Also, it is known that ${\tan ^{ - 1}}\left( {\tan x} \right)$ is equal to $x$.
Therefore, the equation ${\tan ^{ - 1}}\left( {\sqrt 3 } \right) = {\tan ^{ - 1}}\left( {\tan x} \right)$ becomes,
${\tan ^{ - 1}}\left( {\sqrt 3 } \right) = x$
Since, the $\dfrac{\pi }{3}$ is the principle value as $\tan \left( {\dfrac{\pi }{3}} \right) = \sqrt 3$.The general solution for the above equation will be
$x = n\pi + \dfrac{\pi }{3},n{\text{ is an integer}}$
The given range on the $x$ is given as $x \in \left( {0,\dfrac{\pi }{2}} \right)$.
The solution set of the intersection of the graphs is $..\dfrac{{ - 2\pi }}{3},\dfrac{\pi }{3},\dfrac{{4\pi }}{3}..$.
But only one value of the solution set lies in the range $\left( {0,\dfrac{\pi }{2}} \right)$.
Since $k$is the number of solution points for the intersection of the graphs $y = \sqrt 3$ and $y = \tan x$ in the range $x \in \left( {0,\dfrac{\pi }{2}} \right)$, we can say $k$ equals 1.
$k = 1$

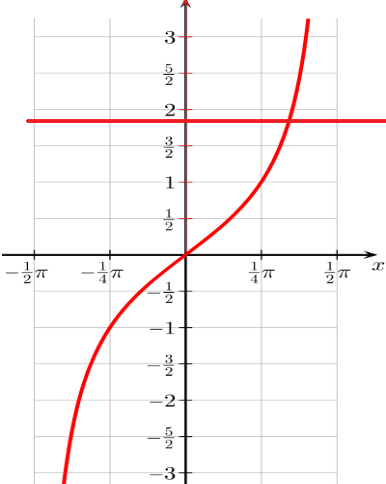
From the graph, there is only one intersection point.

Note: The general solution for the equation $x = {\tan ^{ - 1}}y$ is $n\pi + \theta$ ,where $\theta$ is the principle solution of the equation $x = {\tan ^{ - 1}}y$. Alternatively the above solution can be solved using a graphing utility, counting the intersection points in the range $x \in \left( {0,\dfrac{\pi }{2}} \right)$ to find the value of $k$.