Question

The line $y = mx + c$ passes through $(2,5)$ and $(4,13)$. Find $m$ and $c$.

Answer 1

To find the value of $m$ and $c$ for the line $y = mx + c$ which passes through $(2,5)$ and $(4,13)$, we will first put the point $(2,5)$ and then $(4,13)$ in the equation of line $y = mx + c$. Putting these points will give two linear equations in terms of $m$ and $c$. We will solve these obtained linear equations to find the value of $m$ and $c$.

Complete step by step answer:
The given two points on coordinate axes are shown below.

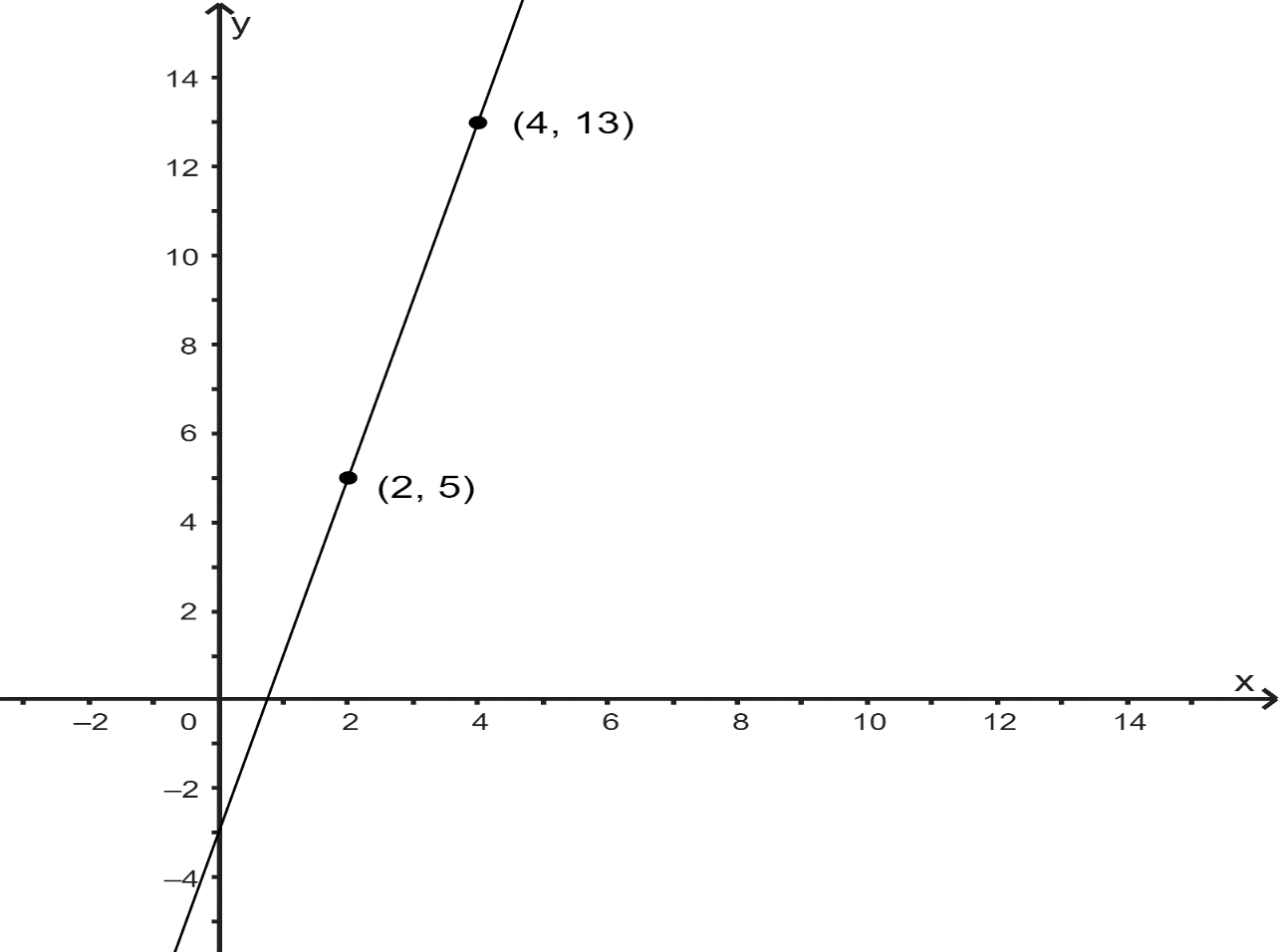
Putting $(2,5)$ in equation $y = mx + c$, we get
$\Rightarrow 5 = m \times 2 + c$
On simplification,
$\Rightarrow 5 = 2m + c$
On rewriting the above equation, we get
$\Rightarrow 2m + c = 5$
Taking $2m$ from L.H.S. to R.H.S., we get
$\Rightarrow c = 5 - 2m - - - (1)$
Putting $(4,13)$ in equation $y = mx + c$, we get
$\Rightarrow 13 = m \times 4 + c$
On simplification,
$\Rightarrow 13 = 4m + c$
On rewriting the above equation, we get
$\Rightarrow 4m + c = 13 - - - (2)$
Putting $(1)$ in $(2)$,
$\Rightarrow 4m + \left( {5 - 2m} \right) = 13$
On solving,
$\Rightarrow 2m + 5 = 13$
Taking $5$ from L.H.S. to R.H.S.
$\Rightarrow 2m = 13 - 5$
On solving we get
$\Rightarrow 2m = 8$
Dividing both the sides by $2$, we get
$\Rightarrow m = \dfrac{8}{2}$
$\Rightarrow m = 4$
Putting the value of $m$ in $\left( 1 \right)$,
$\Rightarrow c = 5 - \left( {2 \times 4} \right)$
On solving,
$\Rightarrow c = 5 - 8$
$\Rightarrow c = - 3$
Therefore, $m$ is $4$ and $c$ is $- 3$ for the line $y = mx + c$ which passes through $(2,5)$ and $(4,13)$.

Note:
We can also solve this problem by first finding the slope ($m$) of the line using given two points and then putting any one of the given points and the obtained value of slope in the equation $y = mx + c$ to find the value of $c$.
As we know that slope ($m$) of the line $y = mx + c$ passing through $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$.
Therefore, slope ($m$) of the line $y = mx + c$ passing through $(2,5)$ and $(4,13)$ is
$\Rightarrow m = \dfrac{{13 - 5}}{{4 - 2}}$
On solving,
$\Rightarrow m = \dfrac{8}{2}$
$\Rightarrow m = 4$
Therefore, $m = 4$.
Now putting $m = 4$ and $(2,5)$ in the equation of the line $y = mx + c$, we get
$\Rightarrow 5 = 4 \times 2 + c$
On simplification,
$\Rightarrow 5 = 8 + c$
Taking $8$ from R.H.S. to L.H.S.
$\Rightarrow 5 - 8 = c$
$\therefore c = - 3$
Hence, the value of $m$ is $4$ and $c$ is $- 3$.