Question

The line $y = mx + 1$is a tangent line to the curve${y^2} = 4x$, then value of ‘m’ will be?

Answer 1

Hint : To find value of ‘m’ we first form a quadratic equation by using value of ‘y’ from given line to other curve and then equating discriminant of quadratic so formed equal to zero to get required value of ‘m’.
Discriminant of a quadratic equation $D = {b^2} - 4ac$

Complete step-by-step answer :
Given, the line $y = mx + 1$ is tangent to the curve${y^2} = 4x$.

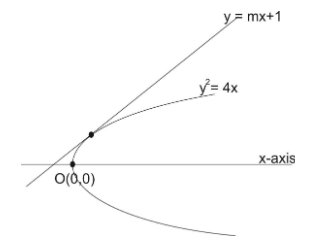
Substituting value of y from line in given equation of parabola. We have
${\left( {mx + 1} \right)^2} = 4x \\\ {m^2}{x^2} + 1 + 2mx = 4x \;$
Shifting all terms to the left side. We have,
${m^2}{x^2} + 2mx - 4x + 1 = 0 \\\ \Rightarrow {m^2}{x^2} + 2(m - 2)x + 1 = 0 \;$
Since, the line is tangent to the given curve.
$\therefore D = 0,\,\,$Where D is discriminant of above quadratic equation.
Also, we know that D =${b^2} - 4ac$. Therefore, from above we have,
${b^2} - 4ac = 0$
Substituting, a, b and c from above formed quadratic.

{\left\\{ {2\left( {m - 2} \right)} \right\\}^2} - 4\left( {{m^2}} \right)\left( 1 \right) = 0 \\\ \Rightarrow 4{\left( {m - 2} \right)^2} - 4{m^2} = 0 \\\ \Rightarrow 4\left( {{m^2} + 4 - 4m} \right) - 4{m^2} = 0 \\\ \Rightarrow 4{m^2} + 16 - 16m - 4{m^2} = 0 \\\ $$\Rightarrow 16 - 16m = 0 \\\ \Rightarrow 16m = 16 \\\ \Rightarrow m = \dfrac{{16}}{{16}} \\\ \Rightarrow m = 1$$

Hence, from above we see that require value of ‘m’ is $1.$

Note : A line is said to be a tangent line to a given curve if it touches only at one point. So, to discuss tangency of a line or condition of tangency. We form a quadratic equation using line and other given curve and then solve by equating discriminant equal to zero of quadratic so formed, as for tangent line there is only one point of contact.