Question

The line $y = 2x$ intersects the ellipse $4x^2 + 9y^2 = 36$ at $P$ and $Q$ and a circle with $PQ$ as diameter intersects the given ellipse at two more points $A$ and $B$. If the equation of $AB$ is $y = \alpha x + \beta$ and the radius of the circle is $r$, then the value of $\sqrt{2}r - \alpha + \beta$ is

Answer 1

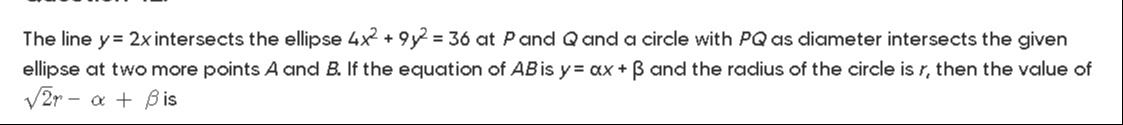
5

Answer 2

Solution:

1. Find P and Q:
   The line is $y=2x$. Substitute in the ellipse $4x^2+9y^2=36$:

   $$4x^2+9(4x^2)=36 \quad\Longrightarrow\quad 40x^2=36 \quad\Longrightarrow\quad x^2=\frac{9}{10}.$$

   Thus, the intersection points are

   $$P\!\left(\frac{3}{\sqrt{10}},\,\frac{6}{\sqrt{10}}\right) \quad \text{and} \quad Q\!\left(-\frac{3}{\sqrt{10}},\,-\frac{6}{\sqrt{10}}\right).$$

2. Circle with PQ as Diameter:
   The center is the midpoint $(0,0)$ and the radius $r$ is the distance of $P$ from the origin:

   $$r=\sqrt{\left(\frac{3}{\sqrt{10}}\right)^2+\left(\frac{6}{\sqrt{10}}\right)^2}=\sqrt{\frac{9+36}{10}}=\sqrt{\frac{45}{10}}=\frac{3}{\sqrt{2}}.$$

   Thus, the circle’s equation is

   $$x^2+y^2=\frac{9}{2}.$$

3. Determine the Equation of AB:
   The circle and ellipse intersect in four points; two are $P$ and $Q$ (on $y=2x$) and the other two, $A$ and $B$, lie on a line $AB: y=\alpha x+\beta$.
   Since $P$ and $Q$ are common to both curves, consider eliminating them between the ellipse and 8 times the circle. Multiply the circle equation by 8:

   $$8(x^2+y^2)=8\cdot\frac{9}{2}\quad\Longrightarrow\quad 8x^2+8y^2=36.$$

   Subtract it from the ellipse:

   $$\bigl[4x^2+9y^2-36\bigr]-\bigl[8x^2+8y^2-36\bigr] = -4x^2+y^2=0.$$

   This factors as:

   $$-4x^2+y^2 = (y-2x)(y+2x)=0.$$

   Since $y=2x$ represents $PQ$, the other line is

   $$y=-2x.$$

   Thus, $\alpha=-2$ and $\beta=0$.

4. Final Computation:
   We are to find

   $$\sqrt{2}r - \alpha + \beta.$$

   Substitute $r=\frac{3}{\sqrt{2}}, \alpha=-2, \beta=0$:

   $$\sqrt{2} \cdot \frac{3}{\sqrt{2}} - (-2) + 0 = 3+2=5.$$

---

Explanation of the Core Steps:

1. Find intersection points $P$ and $Q$ of $y=2x$ and the ellipse.
2. Determine the circle with $PQ$ as diameter (center at origin, $r=\frac{3}{\sqrt{2}}$).
3. Subtract a suitable multiple of the circle’s equation from the ellipse to factor out the line $PQ$ and obtain the chord $AB$ as $y=-2x$.
4. Substitute $\alpha=-2$, $\beta=0$, and $r$ in the expression $\sqrt{2}r - \alpha + \beta$.

---