Question

The line $x - b + \lambda y = 0$ cuts a parabola ${y^2} = 4ax$at $P(a{t_1}^2,2a{t_1})$ and$Q(a{t_2}^2,2a{t_2})$. If $b \in [2a,4a]$ and$\lambda \in \Re$, then ${t_1}{t_2}$ belongs to
A) $[ - 4, - 2]$
B) $[ - 4, - 3]$
C) $[ - 3, - 2]$
D) None of these

Answer 1

Here we are going to consider a point in the parabola and substitute it in the given line and form a quadratic equation from it and using the relation between roots and coefficient we will find the required range.

Formula used:
Any point on a parabola of equation ${y^2} = 4ax$can be taken as$(a{t^2},2at)$.
Let us consider, $\alpha ,\beta$ be two roots of a quadratic equation$a{x^2} + bx + c = 0$, then from the relation between roots and coefficient we get, $\alpha + \beta = \dfrac{{ - b}}{a}$ and$\alpha \beta = \dfrac{c}{a}$.

Complete step by step solution:
The diagrammatic representation of given equations is,

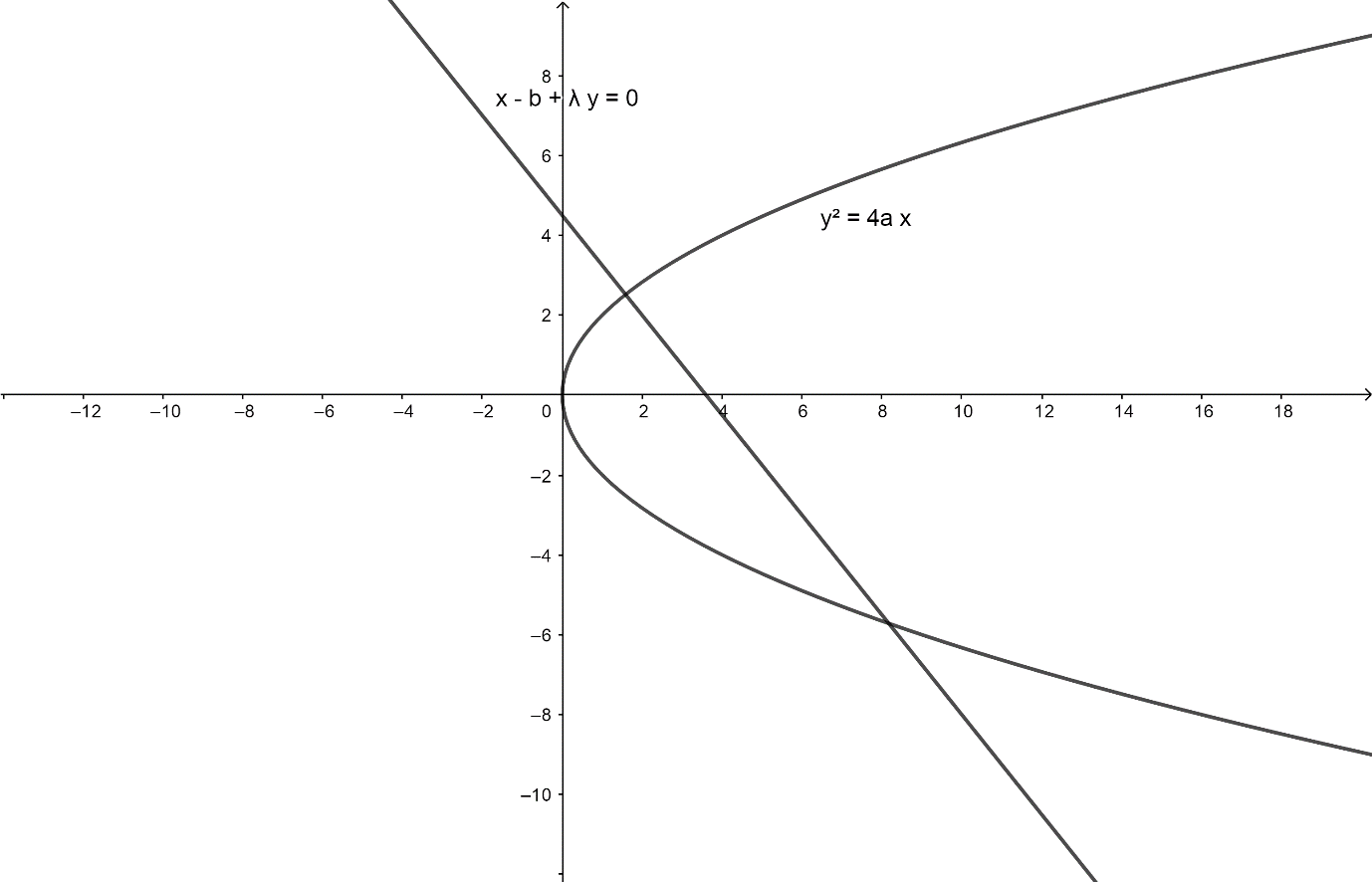
It is given that, the line $x - b + \lambda y = 0$ cuts a parabola ${y^2} = 4ax$at $P(a{t_1}^2,2a{t_1})$ and$Q(a{t_2}^2,2a{t_2})$.
It is given also that, $b \in [2a,4a]$ and$\lambda \in \Re$.
Now, we have to find out the range of${t_1}{t_2}$.
We know that, the any point on a parabola ${y^2} = 4ax$can be taken as $(a{t^2},2at)$
Since, the line $x - b + \lambda y = 0$ cuts a parabola ${y^2} = 4ax$at $(a{t^2},2at)$
Let us substitute $x = a{t^2}y = 2at$ in the equation of the line we get,
$a{t^2} - b + \lambda (2at) = 0$
Let us rearrange the expression and mark it as equation (1) we get,
$a{t^2} + \lambda (2at) - b = 0$… (1)
Since, the line $x - b + \lambda y = 0$ cuts a parabola ${y^2} = 4ax$at $P(a{t_1}^2,2a{t_1})$ and$Q(a{t_2}^2,2a{t_2})$, ${t_1}\& {t_2}$ be the roots of the above equation (1).
Hence, by the relation between roots and coefficient given in the hint we get,
${t_1}{t_2} = \dfrac{{ - b}}{a}$
Also it is given that, the range of $b$ is $[2a,4a]$ which means that $b$ lies between $2a$ and $4a$,
That is $2a \le b \le 4a$
Let us divide the above inequality by $a$ we get,
$2 \le \dfrac{b}{a} \le 4$
Also let us multiply $- 1$ with each element in the inequality we get,
$- 4 \le \dfrac{{ - b}}{a} \le - 2$
We initially have that, ${t_1}{t_2} = \dfrac{{ - b}}{a}$
So the above inequality becomes $- 4 \le {t_1}{t_2} \le - 2$
So, the range of ${t_1}{t_2}$ is $[ - 4, - 2]$
Hence ${t_1}{t_2} \in [ - 4, - 2]$.

$\therefore$The correct option is (A) $[ - 4, - 2]$

Note:
Let us consider, $x$ be a real number in the range$[a,b]$, so the range of $- x$ is$[ - b, - a]$.
If the negative sign will be added, the range will be interchanged.
In other words, the inequality changes when it is multiplied by -1, that is if inequality is multiplied by -1 if there is greater than then it is changed to less than and vice versa.