Question

The line $x - 7 = 0$ is
A.Parallel to $y$-axis.
B.Parallel to $x$-axis.
C.Passing through the origin.
D.None of these.

Answer 1

We will first solve the given equation to find the value of $x$. We will then form a table to find the value of $x$ with respect to $y$. We will then draw a graph using the table to find the nature of the line whether it is parallel to $x$-axis, $y$-axis or passing through the origin.

Complete step by step solution:
We will first solve the given equation to find the value of $x$. We will then form a table to find the value of $x$ with respect to $y$. We will then draw a graph using the table to find the nature of the line whether it is parallel to $x$-axis, $y$-axis or passing through the origin.

$x$	7	7	7	7	7	7
$y$	$- 2$	$- 1$	0	1	2	3

Hence, from this table it is proved that for any value of $y$ (both negative and positive), $x$ will always hold the same value.
Hence, the graph of the line $x - 7 = 0$ will be:

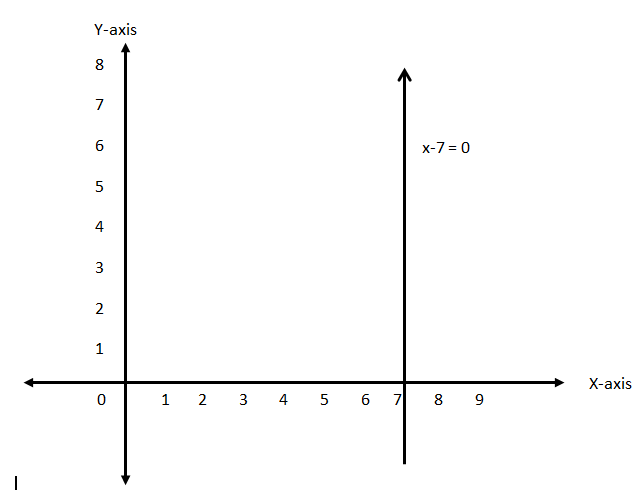
From this graph, we can say that it holds a constant value of $x = 7$ and it is parallel to $y$-axis.

Hence, option A is the correct option.

Note: Since, the line is parallel to $y$-axis, clearly, it should be perpendicular to $x$-axis. Also, from the graph, the line makes a right angle with $x$-axis hence, it is perpendicular to it. The equation of a straight line parallel to $y$-axis at a distance ‘$a$’ from it is $x = a$.
Also, the equation of a straight line parallel to $x$-axis at a distance ‘b’ from it is $y = b$. The equation of $y$-axis is $x = 0$ , because $y$-axis is parallel to itself at a distance 0 from it. Similarly, the equation of $x$-axis is $y = 0$ , because $x$-axis is parallel to itself at a distance 0 from it.