Question
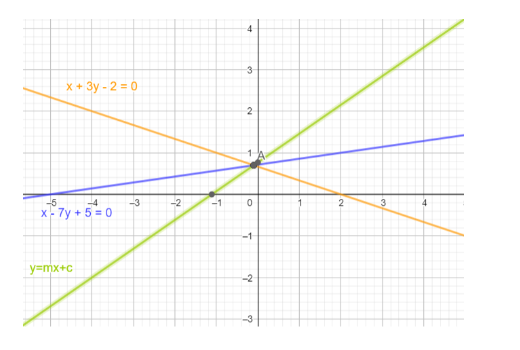
Question: The line x+3y-2= 0 bisects the angle between a pair of lines one of which has the equation x-7y+5 =0...
The line x+3y-2= 0 bisects the angle between a pair of lines one of which has the equation x-7y+5 =0. Find the equation of the other line.
Solution
Hint: Assume that the equation of the line is y = mx+c. Use the fact that the angle between two lines of slopes m1 and m2 is given by ϕ=tan−11+m1m2m1−m2. Hence find the angle between the lines x+3y-2 = 0 and x-7y+5 = 0 and also the angle between the lines x+3y-2=0 and y = mx+c. Equate the two angles and hence form an equation in m. Solve for me and hence find the slope of the line. Use the fact that the pair of lines and the angle bisector of the pair are concurrent. Hence the line y = mx+c must pass through the point of intersection of x-7y+5 = 0 and x+3y-2 = 0. Hence find the value of c and hence find the equation of the line.
Complete step-by-step answer:
Let the equation of the line be y = mx+c.
We know that the slope of the line ax+by+c = 0 is given by m=b−a
Hence, we have
Slope of the line x-7y+5 = 0 is −7−1=71 and the slope of the line x+3y -2 = 0 is 3−1
We know that the angle between two lines of slopes m1 and m2 is given by ϕ=tan−11+m1m2m1−m2
Hence, we have
Angle between the lines x-7y+5 = 0 and x+3y -2 = 0 is ϕ=tan−11+(71)(3−1)71−(−31)=tan−121−110=tan−1(21)
Also, we have
Angle between the lines x-7y+5 and y = mx+c is given by
θ=tan−11+7mm−71=tan−1m+77m−1
But since the line x-7y+5 = 0 is the angle bisector of the lines x+3y-2 =0 and y = mx+c, we have
ϕ=θ
Hence, we have
tan−1m+77m−1=tan−121
Since tan−1x is one-one, we have
m+77m−1=21
We know that if ∣x∣=a,a≥0, then x=±a
Hence, we have
m+77m−1=±21
Taking the positive sign, we get
m+77m−1=21
Cross multiplying, we get
14m−2=m+7
Hence, we have
13m=9⇒m=139
Taking the negative sign, we get
m+77m−1=2−1
Cross multiplying, we get
14m−2=−m−7
Hence, we have
15m=−5⇒m=3−1
Finding the coordinates of point of intersection of x+3y- 2 = 0 and x-7y+5 = 0
We have
x+3y -2 = 0 (i)
x-7y+5=0 (ii)
Subtracting equation (i) from equation (ii), we get
−10y+7=0⇒y=107
Substituting the value of y in equation (ii), we get
x−1049+5=0⇒x=10−1
Hence, we have A≡(10−1,107)
When m=139, we have
Equation of the line is ‘y=139x+c
Since the line passes through A, we have
107=130−9+c⇒c=13091+9=1310
Hence, the equation of the line is
y=139x+1310
Multiplying both sides by 13, we get
13y=9x+10
When m=3−1, we have
Equation of the line is y=−31x+c
Since the line passes through A, we have
107=301+c⇒c=3021−1=32
Hence, the equation of the line is
y=3−1x+32
Multiplying both sides by 3, we get
3y=−x+2
This is the same as equation (i) and hence is rejected.
Hence the equation of the line is 13y=9x+10
Note: Alternative solution:
We know that the equation of the line which is concurrent to two lines L1=0 and L2=0 is given by L1+L2=0
Hence, we have
Equation of the line is
x+3y−2+(x−7y+5)=0⇒x(1+)+y(3−7)−2+5=0
Since the slope of the line is 139(Proved above), we have
−3−71+=139⇒13+13=63−27⇒50=40⇒=54
Hence the equation of the line is
x(1+54)+y(3−754)−2+5(54)=0⇒9x−13y+10=0
which is the same as obtained above.
