Question

The line segment joining the points (3, -4) and (1,2) is trisected at the points P and Q. If the coordinates of P and Q are (p, -2) and ( $\dfrac{5}{3}$, q) respectively, find the values of p and q.

A. p = $\dfrac{7}{3}$, q = – 3
B. p = $\dfrac{7}{3}$, q = 0
C. p = $\dfrac{5}{3}$, q = 0
D. None of these

Answer 1

Hint: In this question to find the values of p and q, we will use the section formula and then check each given option to find out which are correct.

Complete step-by-step answer:

Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is

x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$

Here we are given two points. Let's say A (3, -4) and B (1,2) make a line segment AB. The line segment AB is trisected at points P and Q. So, we will apply section formula both at point P and Q. As, P divides line segment AB in ratio 1:2.

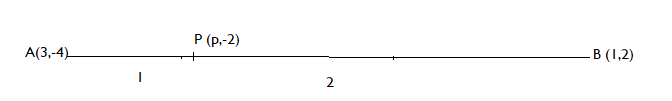
So, applying section formula at point P (p, -2), we get
x – coordinate of P = $\dfrac{{1(1){\text{ + 2(3)}}}}{3}$ = $\dfrac{7}{3}$
$\Rightarrow$ p = $\dfrac{7}{3}$
As, Q divides the line segment AB in the ratio 2:1.

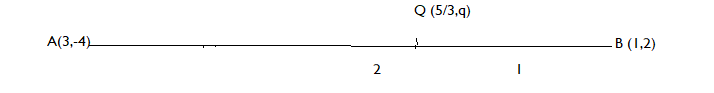
Applying section formula at point Q ( $\dfrac{5}{3}$, q), we get
y – coordinate of Q = $\dfrac{{2(2){\text{ + 1( - 4)}}}}{3}$ = 0
$\Rightarrow$ q = 0
So, the correct option will be B.

Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.