Question

The line segment joining the points (1, 2) and (k, 1) is divided by the line $3x+4y-7=0$ in the ratio 4:9, then the value of k is
(a) 2
(b) -2
(c) 3
(d) -3

Answer 1

Hint: Here, we will use the section formula to find the point where the line cuts the line segment joining the points (1, 2) and (k, 1). The obtained point will certainly lie on the line $3x+4y-7=0$. Putting that point in the equation of the given line will give us the value of k.

Complete step-by-step answer:

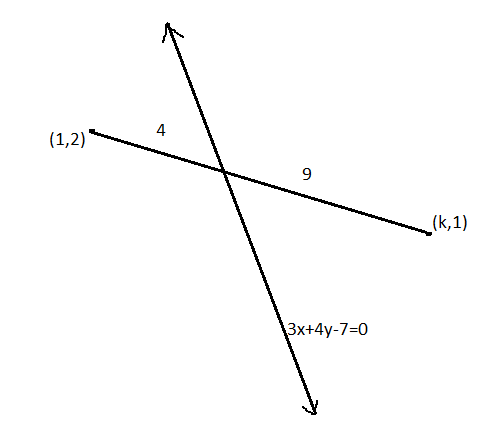
The section formula tells us the co-ordinates of the point which divides a given line segment into two parts such that their lengths are in the ratio m:n. If a point P (x, y) lies on line segment AB ( A and B are the end points of the line segment) and satisfies AP: BP = m: n, then we can say that P divides AB internally in the ratio m:n. The point of division has the coordinates:
$P=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)..........\left( 1 \right)$ , where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the coordinates of the points A and B respectively.
Here, the end points of the line segment are given as (1, 2) and (k, 3).
The ratio in which it is divided by the line $3x+4y-7=0$ is equal to 4:9.
So, we have m=4 and n =9.
On putting the given values in equation (1), we get:
$\begin{aligned} & P=\left( \dfrac{4\times k+9\times 1}{4+9},\dfrac{4\times 1+9\times 2}{4+9} \right) \\\ & \Rightarrow P=\left( \dfrac{4k+9}{13},\dfrac{22}{13} \right) \\\ \end{aligned}$
Since, the point P lies on the given line $3x+4y-7=0$. So, we can satisfy the point with this line by putting the values of coordinates of the line at the place of x and y in the equation of the line:
$\begin{aligned} & 3\times \left( \dfrac{4k+9}{13} \right)+4\times \dfrac{22}{13}-7=0 \\\ & \Rightarrow \dfrac{12k+27}{13}+\dfrac{88}{13}-7=0 \\\ & \Rightarrow \dfrac{12k+27+88-91}{13}=0 \\\ & \Rightarrow 12k+24=0 \\\ & \Rightarrow k=\dfrac{-24}{12} \\\ & \Rightarrow k=-2 \\\ \end{aligned}$
So, the value of k is -2.
Hence, option (b) is the correct answer.
Note: Students should note here that the line segment joining the points (1, 2) and (k, 1) is divided internally by the given line in the ratio of 4:9. So, we have to use the formula for internal division only. Using the formula of external division instead of internal division is a chance of mistake.