Question

The line segment joining the midpoints of two sides of a triangle is parallel to the third side.

Answer 1

Hint: In this question, we will draw the triangle and then draw a line segment parallel to third sides and extend the line segment to meet this line at some point. Then we will use the AAS rule and properties of a parallelogram to prove. Since we know that the opposite sides of a parallelogram are parallel and equal, the proof will be simple.

Complete step by step answer:
Let us assume that ABC is a triangle where E and F are the midpoint of AB and AC respectively.

First, we will draw the triangle ABC and then draw a line segment parallel to AB and extend the EF to meet this line at D.

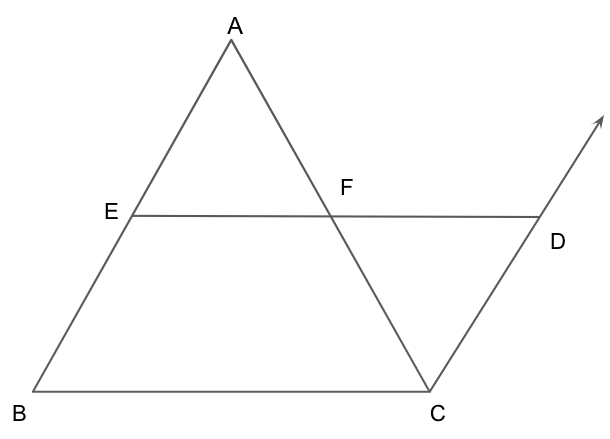
Since we know that the line segment AB is parallel to CD with transversal ED.

Using the fact that $\angle {\text{AEF}}$ and $\angle {\text{CDF}}$ are alternate angles, we get

$\Rightarrow \angle {\text{AEF}} = \angle {\text{CDF ......eq.(1)}}$

In triangles $\Delta {\text{AEF}}$ and $\Delta {\text{CDF}}$, we have

Since $\angle {\text{AFE}}$and $\angle {\text{CFD}}$ are vertically opposite angles, $\angle {\text{AFE}} = \angle {\text{CFD}}$.

As F is mid point of the line segment AC, we have ${\text{AF}} = {\text{CF}}$.

We know that in AAS rule, when two angles and a side of two triangles are the same, then both triangles are congruent with each other.

Using the above AAS rule, we get
$\therefore \Delta {\text{AEF}} \cong \Delta {\text{CDF}}$

Being the corresponding parts of congruent triangles $\Delta {\text{AEF}}$ and $\Delta {\text{CDF}}$, the line segments EA and DC are equal.

But E is midpoint of AB, ${\text{EA}} = {\text{EB}}$.

Hence, we have from above that ${\text{EB}} = {\text{DC}}$.

Now in EBCD, we have that ${\text{EB}} = {\text{DC}}$ and ${\text{EB||DC}}$.

Thus, we have found out the one pair of opposite sides is equal and parallel.

Therefore, EBCD is a parallelogram.

Since opposite sides of a parallelogram are parallel, so the line segments ED and BC are parallel.

Hence, proved.

Note: In such types of problems, students should draw a figure first and also construct a line parallel to one side of the triangle. Then prove that quadrilateral is also a parallelogram and we know opposite sides of a parallelogram are parallel and equal.