Question

The line segment joining points A (2,1) and B (5,-8) is trisected at the point P and Q. P is nearer to A. If P also lies on the line 2x-y+k=0, find the value of k.

Answer 1

Hint: The points of trisection divide the line segment in the ratio 1:2 and 2:1. Hence P divides AB in the ratio of 1:2 and Q divides AB in the ratio of 2:1. Use section formula which states that the coordinates of the point P which divides $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio of m:n is given by $\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$. Hence find the coordinates of point P. Also, as point P lies on 2x-y+k, it must satisfy the equation. Hence find the value of k so that p satisfies the above equation of the line.

Complete step-by-step solution -

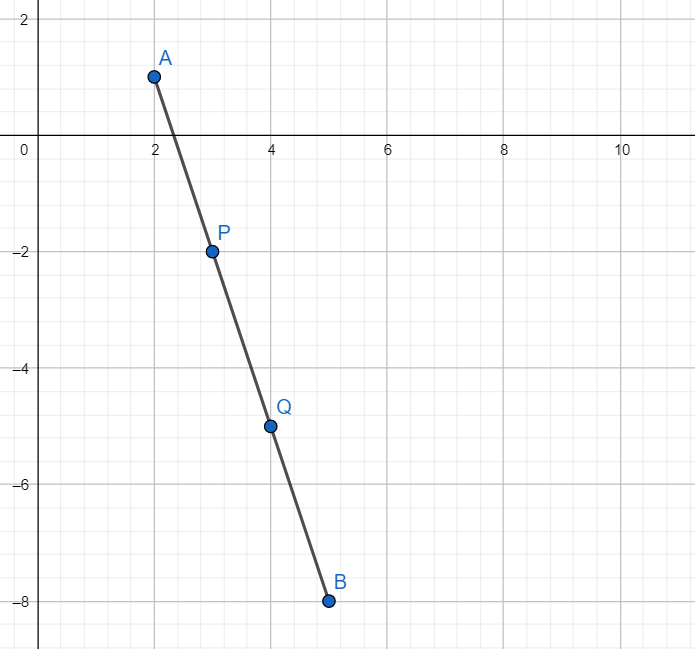
As P and Q are the points of trisection, we have
AP = PQ = QB.
Hence we have $\dfrac{AP}{PB}=\dfrac{AP}{2AP}=\dfrac{1}{2}$
Hence P divides AB in the ratio of 1:2.
Similarly Q divides AB in the ratio of 2:1
Finding coordinates of P:
that the coordinates of the point P which divides $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio of m:n is given by $\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$
Here ${{x}_{1}}=2,{{x}_{2}}=5,{{y}_{1}}=1$ and ${{y}_{2}}=-8$ and m = 1 and n= 2
Hence we have
$P\equiv \left( \dfrac{1\times 5+2\times 2}{1+2},\dfrac{1\times \left( -8 \right)+2\times 1}{1+2} \right)=\left( \dfrac{9}{3},\dfrac{-6}{3} \right)=\left( 3,-2 \right)$
Finding coordinates of Q:
that the coordinates of the point P which divides $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio of m:n is given by $\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$
Here ${{x}_{1}}=2,{{x}_{2}}=5,{{y}_{1}}=1$ and ${{y}_{2}}=-8$ and m = 2 and n= 1
Hence we have
$Q\equiv \left( \dfrac{2\times 5+1\times 2}{1+2},\dfrac{2\times \left( -8 \right)+1\times 1}{1+2} \right)=\left( \dfrac{12}{3},\dfrac{-15}{3} \right)=\left( 4,-5 \right)$

Also, since P lies on 2x-y+k = 0, P must satisfy its equation.
Hence we have
2(3)-(-2)+k = 0
i.e. k =-8
Hence the value of k is -12.

Note: Alternative solution: Best method:
The ratio in which the line ax+by+c=0 divides the line segment joining points $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $-\dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{a{{x}_{2}}+b{{y}_{2}}+c}$ (Remember)
Hence the ratio in which 2x-y+k = 0 divides the line segment joining A (2,1) and B (5,-8) is given by
$-\dfrac{2\left( 2 \right)-1+k}{2\left( 5 \right)-\left( -8 \right)+k}=-\dfrac{3+k}{18+k}$
Since the line 2x-y+k = 0 intersects AB at P which divides AB in the ratio 1:2, we have
$-\dfrac{3+k}{18+k}=\dfrac{1}{2}$
Cross multiplying, we get
$\begin{aligned} & -6-2k=18+k \\\ & \Rightarrow 3k=-24 \\\ & \Rightarrow k=-8 \\\ \end{aligned}$