Question

The line segment joining $\left( {2, - 3} \right)$ and $\left( {5,6} \right)$ is divided by $x$ axis in the ratio:
A. 2:1
B. 3:1
C. 1:2
D. 1:3

Answer 1

Let the coordinates of the point on $x$ axis be $\left( {h,0} \right)$ where the line segment intersects the $x$ axis. Let the required ratio be $1:m$. Then, use the section formula and the given values to determine the value of $m$ and hence the required ratio.

Complete step-by-step answer:
We are given that the line segment joins $\left( {2, - 3} \right)$ and $\left( {5,6} \right)$ which divides the $x$ axis in certain ratios.
Let the ratio be $1:m$
And the coordinates on the $x$ axis be $\left( {h,0} \right)$

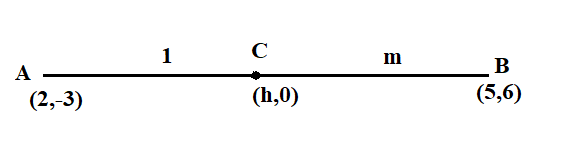
Now, apply the ratio formula on $y$ coordinate of the given line.
If the points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are divided by point $\left( {x,y} \right)$ in ratio $p:q$, then the value of the coordinates $\left( {x,y} \right)$ is $\left( {x = \dfrac{{p\left( {{x_2}} \right) + q\left( {{x_1}} \right)}}{{p + q}},y = \dfrac{{p\left( {{y_2}} \right) + q\left( {{y_1}} \right)}}{{p + q}}} \right)$
Then, from the line AB, we have,
$\left( {h = \dfrac{{1\left( 5 \right) + m\left( { 2} \right)}}{{1 + m}},0 = \dfrac{{1\left( 6 \right) + m\left( { - 3} \right)}}{{1 + m}}} \right)$
From the $y$ coordinate we have,
$\Rightarrow 0 = \dfrac{{6 - 3m}}{{1 + m}} \\\ \Rightarrow 6 - 3m = 0 \\\ \Rightarrow 3m = 6 \\\$
Divide both equations by 3
$\Rightarrow$ $m = 2$
Hence, the ratio is 1:2
Thus, option C is correct.
Note: The coordinates on the $x$ axis is of the form $\left( {h,0} \right)$ whereas the coordinates on the $y$ axis is of the form $\left( {0,k} \right)$. Here, we have used the section formula, if the points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are divided by point $\left( {x,y} \right)$ in ratio $p:q$, then the value of the coordinates $\left( {x,y} \right)$ is $\left( {x = \dfrac{{p\left( {{x_2}} \right) + q\left( {{x_1}} \right)}}{{p + q}},y = \dfrac{{p\left( {{y_2}} \right) + q\left( {{y_1}} \right)}}{{p + q}}} \right)$.