Question

The line joining the points ${\text{(}} - {\text{6}},8{\text{)}}$ and ${\text{(8,}} - {\text{6)}}$ is divided into four equal parts; find the coordinates of the points of section.

Answer 1

Hint: - Here, we use bisector formulas to find midpoints.

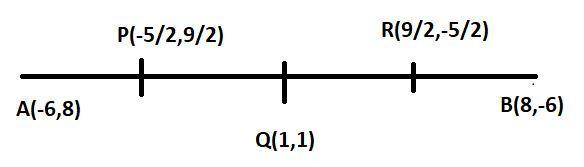
Let ${\text{A(}} - {\text{6,8)}}$ and ${\text{B(8,}} - {\text{6)}}$ and ${\text{P,Q,R}}$ divides ${\text{AB}}$ in four equal parts ${\text{Q}}$ divides ${\text{AB}}$ in ${\text{1:1}}$,so ${\text{Q}}$ is the midpoint of ${\text{AB}}$.

So coordinates of ${\text{Q}}$ are $\dfrac{{ - {\text{6 + 8}}}}{2}{\text{,}}\dfrac{{{\text{8}} - {\text{6}}}}{2}$
$\Rightarrow {\text{Q}}(1,1)$

Similarly ${\text{P}}$ is the midpoint of ${\text{AQ}}$

So coordinates of ${\text{P }}$ are $\dfrac{{ - {\text{6 + 1}}}}{2},\dfrac{{8+1}}{2}$
$\Rightarrow {\text{P}}\left( { - \dfrac{5}{2},\dfrac{9}{2}} \right)$

And now ${\text{R }}$ is the midpoint of ${\text{QB}}$

So coordinates of ${\text{R}}$ are $\dfrac{{1 + 8}}{2},\dfrac{{1 - 6}}{2}$
$\Rightarrow {\text{R }}\left( {\dfrac{9}{2},\dfrac{{ - 5}}{2}} \right)$
The points which divide the line in four equal parts are $\left( { - \dfrac{5}{2},\dfrac{9}{2}} \right);(1,1);\left( {\dfrac{9}{2},\dfrac{{ - 5}}{2}} \right)$

Note:-Whenever we face such types of questions it is better to denote the coordinate by letter and then bisect the first line and after that bisect that line. Which are made by the bisector of the first line.